Tìm một số,mà những số tạo ra số đó cộng số đó bằng 1559
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tổng đúng là số thập phân có hai chữ số ở phần thập phân nên số thập phân bị quên dấu phẩy là số có hai chữ số ở phần thập phân.
Khi số thập phân có hai chữ số ở phần thập phân bị quên dấu phẩy thì được số mới gấp 100 lần số ban đầu.
Tổng mới hơn tổng cũ bằng: 100 - 1 = 99 ( số thập phân ban đầu)
Tổng mới hơn tổng cũ là: 1559 - 49,25 = 1509,75
Số thập phân ban đầu là: 1509,75 : 99 = 15,25
Số tự nhiên là: 49,25 - 15,25 = 34
Đáp số: Số tự nhiên là 34
Số thập phân là 15,25
thử lại kết quả ta có:
Tổng đúng là: 34 + 15,25 = 49,25 (ok)
Tổng sai là: 34 + 1525 = 1559 (ok)
Vậy kết quả bài toán là đúng

Ta gọi số đó là x :
x : 6 + 6 = 6 x 8
x : 6 + 6 = 48
x = 48 - 6
x = 42
x = 42 x 6
x = 252

Sau khi trừ hai thì số đó sẽ là :
13 - 5 = 8
Số Hà đã nghĩ ra là :
8 + 2 = 10
Đáp số : 10

a, gọi số cần tìm là a thì ta có ( a+12):2=9
a+12=18
a=6
b, gọi số cần tìm là b thì ta có (b+30):2=28
b+30=56
b=26
(a) Tổng hai số đó là: 9.2= 18
Số đó là: 18-12=6
(b) Tổng hai số đó là: 28. 2= 56
Số đó là: 56-30=26

Gọi ba số đã cho u1,u2,u7 theo thứ tự là ba số của một cấp số cộng (un) và v1,v2, v3 của cấp số nhân (vn) . Theo giả thiết Ta có hệ:
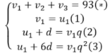
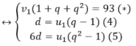
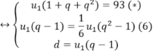
Giải phương trình (6)
( 6 ) ⇔ u 1 q − 1 = 1 6 u 1 q − 1 q + 1 ⇔ u 1 q − 1 = 0 ( l o a i ) 1 = 1 6 q + 1
Thay vào (*), ta được
u 1 1 + 5 + 5 2 = 93 ⇔ u 1 = 3 = v 1
Suy ra
u 2 = u 1 . q = 3.5 = 15 = v 2 u 3 = u 1 . q 2 = 3.25 = 75 = v 3
Vậy tích ba số v 1 . v 2 . v 3 = 3.15.75 = 3375
Đáp án A

Gọi 3 số đã cho là \(u_1;u_2;u_3\), theo thứ tự là 3 số của một cấp số cộng
Còn cấp số nhân \(\left(v_n\right)\). Theo giả thiết ta có hệ :
\(\Leftrightarrow\begin{cases}v_1+v_2+v_3+v_4=93\left(a\right)\\v_1=u\left(1\right)_1\\u_1+d=v_1q\left(2\right)\\u_1+2d=v_1q^2\left(3\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}v_1\left(1+q+q^2\right)=93\left(a\right)\\d=u_1\left(q-1\right)\left(1V2\right)\left(4\right)\\6d=u_3-u_1=u_1\left(q^2-1\right)\left(2V3\right)\left(5\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}u_1\left(1+q+q^2\right)=93\left(a\right)\\u_1\left(q-1\right)=\frac{1}{6}u_1\left(q^2-1\right)\left(4V5\right)\left(6\right)\\d=u_1\left(q-1\right)\end{cases}\)
Từ (1) và (2) cho ta phương trình (4). Còn từ (2) và (3) cho phương trình (5). Mặt khác ừ (4) và (5) cho phương trình (6)
Do \(u_1\ne0,q\ne1\Rightarrow\left(6\right)\Leftrightarrow1=\frac{1}{6}\left(q+1\right)\Leftrightarrow q=5\)
Theo (a) : \(v_1+5v_1+25v_1=93\Leftrightarrow u_1=3\)
Vậy 3 số cần tìm là : 3,15,75

số đó là: -100.000.000 + 100.000.000 = 0!!!!!!!!!!!!!!!!
nhớ k cho mình nha
Câu trả lời hay nhất: Cách Tiểu học:
Giải
Số tự nhiên phải tìm không thể là số có ba chữ số, vì cho dù là 999 thì:
999 + 9 + 9 + 9 = 1026 < 1159
Số đó bé hơn 1159. Vậy nó là số có bốn chữ số, có dạng abcd và ta có:
abcd + a + b + c + d = 1159
( Bạn trình bày theo hàng dọc cho dễ làm )
Ta xác định được a = 1 và b = 1
Từ đó ta có:
11cd + 1 + 1 + c + d = 1159
* Nếu phép cộng ở hàng đơn vị không qua 10 thì c = 5 và d = 1
Số đó là : 1151
Thử lại:
1151 + 1 + 1 + 5 + 1 = 1159
* Nếu phép cộng ở hàng đơn vị qua 10 thì c = 4 hoặc 3, khi đó d x 2 = 15 - 4 = 11 hoặc d x 2 = 25 - 3 = 22 đều không xảy ra được.
Vậy số cần tìm là 1151
Đáp số : 1151
Đề bài cho tổng của chúng bằng 1559 mà sao lại là 1159.
Mà vẫn chọn đúng vậy?