Question

[Trúc Nguyễn]

cho hàm số \(y=-2x^2\) có đồ thị (p)

1 vẽ (p) trên một hệ trục toạ độ vuông góc

2 gọi \(A\left(-\dfrac{2}{3},-7\right);B\left(2,1\right)\) 

a, viết phương tình đường thẳng AB

b, xác định toạ độ các giao điểm của đường thẳng AB và (P)

3 tìm điểm trên (p)có tổng hoành độ và tung độ của nó bằng 6

Answer 1

[Phạm Uyên]

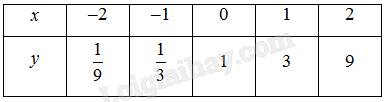
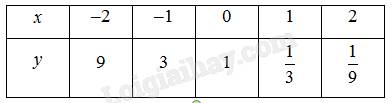
1. Cái này chắc bạn tự vẽ được nhỉ?

2. 

a, -Gọi pt đường thẳng cần tìm là (d): y=ax+b (a\(\ne\)0)

- Vì A (\(\dfrac{-2}{3}\); -7) và B(2; 1) \(\in\) (d)

=> hệ pt: (1):    -7= \(\dfrac{-2}{3}\)a+b

               (2):      1= 2a+b

(bạn tự giải hệ nhé) => a= 3 (tmđk); b=-5

=> pt đường thẳng cần tìm: y=3x-5

b, - Xét pt hoành độ giao điểm của (P) và (d):

=> -2x\(^2\)=3x-5

=> x=1 hoặc x=-\(\dfrac{5}{2}\)

- Với C, D là hai giao điểm của (P) và (d):

+ Khi x=1 => y=-2 => C (1; -2)

+ Khi x=-\(\dfrac{5}{2}\) => y= -\(\dfrac{25}{2}\) => D (-\(\dfrac{5}{2}\); -\(\dfrac{25}{2}\))

3. - Để tổng hoành độ và tung độ của điểm cần tìm bằng 6

=> x+y=6

mà điểm đó thuộc (P) nên thay y= -2x\(^2\) vào pt, ta được:

x-2x\(^2\)=6 <=> -2x\(^2\)+x-6=0

=> vô nghiệm

=> không có điểm nào nằm trên (P) có tổng hoành độ và tung độ bằng 6