Mn giải giúp bài này nha (chỉ cần giải giúp mk phần D thôi ).Arigato mn(xin đừng bơ mk nữa )
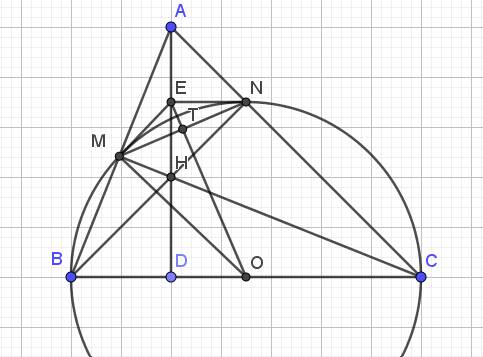
Cho tam giác ABC nhọn,đường tròn tâm O đường kính BC cắt AB ở M,cắt AC ở N.Gọi H là giao điểm của BN và CM.
a)CM:AHvuông góc BC
b)Gọi E là trung điểm AH.CM: ME là tiếp tuyến của đường tròn tâm O
c)CM:\(MN.OE=2ME.MO\)
d)Giả sử AH=BC.Tính tan BÂC

Câu hỏi của Nhóc vậy - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
em cảm ơn