Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB=10cm,cạnh bên SA=12cm.
a) tính đường chéo AC
b) tính thể tích chóp tứ giác đều S.ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 6 2021
a) Áp dụng định lý Pytago, ta được:
AC2=AB2+BC2=2AB2AC2=AB2+BC2=2AB2
⇒AC=AB√2=10√2cm⇒AC=AB2=102cm
b) Gọi MM là trung điểm ABAB
⇒MA=MB=MO=5cm⇒MA=MB=MO=5cm
⇒SM⊥AB⇒SM⊥AB (ΔSAB∆SAB cân tại SS)
⇒SM=√SA2−AM2=√122−52=√119cm⇒SM=SA2−AM2=122−52=119cm
⇒SO=√SM2−OM2=√119−52=√94cm⇒SO=SM2−OM2=119−52=94cm
⇒VS.ABCD=13.SABCD.SO=13.AB2.SO=102.943=94003cm3
9 tháng 5 2023
a: \(AC=\sqrt{10^2+10^2}=10\sqrt{2}\left(cm\right)\)
b: AO=5căn 2(cm)
=>\(SO=\sqrt{SA^2+AO^2}=\sqrt{194}\left(cm\right)\)
CM
28 tháng 2 2019
Chọn đáp án A
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
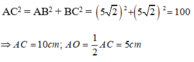
Áp dụng định lí Pytago vào tam giác vuông SAO có:
S O 2 = S A 2 - A O 2 = 13 2 - 5 2 = 144 nên SO = 12cm
CM
5 tháng 12 2019
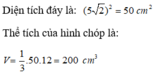
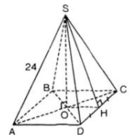
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 -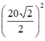 
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
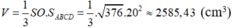
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 –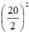 
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
CM
23 tháng 4 2018
Đáp án B
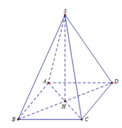
Ta có: 2 B H 2 = a 3 2 ⇒ B H 2 = 3 a 2 2
S H = S B 2 − B H 2 = 2 a 2 − 3 a 2 2 = a 2
Thể tích khối chóp S.ABCD là:
V = 1 3 . S H . S A B C D = 1 3 . a 2 . a 3 2 = a 3 2