Trong mặt phẳng tọa độ $Oxy$ cho Parabol $(P):y=x^2$, trên $(P)$ lấy hai điểm $A(-1;1),B(3;9)$.
a) Tính diện tích tam giác $OAB$.
b) Xác định điểm $C$ thuộc cung nhỏ $AB$ của $(P)$ sao cho diện tích tam giác $ABC$ lớn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
vậy: A(1;1); B(2;4)
Gọi H là tọa độ của hình chiếu vuông góc kẻ từ O xuống AB
O(0;0); H(x;y); A(1;1); B(2;4)
\(\overrightarrow{OH}=\left(x;y\right);\overrightarrow{AB}=\left(1;3\right)\)
Vì OH vuông góc với AB nên \(x\cdot1+y\cdot3=0\)
=>x+3y=0
Ta có: \(\overrightarrow{AH}=\left(x-1;y-1\right);\overrightarrow{AB}=\left(1;3\right)\)
mà A,H,B thẳng hàng
nên \(\dfrac{x-1}{1}=\dfrac{y-1}{3}\)
=>3x-3=y-1
=>3x-y=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-y=2\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x-3y=6\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}10x=6\\x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\3y=-x=-\dfrac{3}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(H\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)
khi m thay đổi
x2 và đường thẳng (d) : y = mx - 
.
CM
10 tháng 1 2019
1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
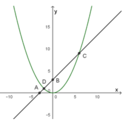
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .
9 tháng 5 2023
a: Thay x=2 vào (P),ta được:
y=2^2/2=2
2: Thay x=2 và y=2 vào (d), ta được:
m-1+2=2
=>m-1=0
=>m=1
a: O(0;0); A(-1;1); B(3;9)
\(OA=\sqrt{\left(-1-0\right)^2+\left(1-0\right)^2}=\sqrt{2}\)
\(OB=\sqrt{\left(3-0\right)^2+\left(9-0\right)^2}=\sqrt{3^2+9^2}=3\sqrt{10}\)
\(AB=\sqrt{\left(3+1\right)^2+\left(9-1\right)^2}=\sqrt{4^2+8^2}=4\sqrt{5}\)
Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{2+90-80}{2\cdot\sqrt{2}\cdot3\sqrt{10}}\)
\(=\dfrac{12}{6\sqrt{20}}=\dfrac{12}{12\sqrt{5}}=\dfrac{1}{\sqrt{5}}\)
=>\(sinAOB=\sqrt{1-\left(\dfrac{1}{\sqrt{5}}\right)^2}=\dfrac{2}{\sqrt{5}}\)
Diện tích tam giác AOB là:
\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB\cdot sinAOB\)
\(=\dfrac{1}{2}\cdot\sqrt{2}\cdot3\sqrt{10}\cdot\dfrac{2}{\sqrt{5}}=3\cdot\dfrac{\sqrt{20}}{\sqrt{5}}=6\)