K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2017
Vì OA là tia phân giác của xOC => xOA=AOC=12.xOCxOA=AOC=12.xOC (1)
Vì OB là tia phân giác của COy => COB=BOy=12.COyCOB=BOy=12.COy (2)
Từ (1) và (2) => xOA+BOy=AOC+BOC=12.xOC+12.COyxOA+BOy=AOC+BOC=12.xOC+12.COy
=> xOA+BOy=AOB=12.(xOC+COy)xOA+BOy=AOB=12.(xOC+COy)
=> 90o=12.xOy90o=12.xOy
=> xOy=90:12xOy=90:12
=> xOy = 90.2 = 180 => là góc bẹt
=> Ox và Oy là 2 tia đối nhau
Vậy Ox và Oy là 2 tia đối nhau
hihi
TN
29 tháng 3 2017
Ta có: \(\widehat{yOz}\)=\(\widehat{xOz}\)-\(\widehat{xOy}\)(vì \(Oy\) nằm giữa \(Ox\) và \(Oz\))
\(\widehat{yOz}\)=\(120^o\)-\(30^o\)=\(90^o\)
Vì \(Om\) là tia phân giác của góc \(xOy\) nên: \(\widehat{mOn}\)=\(30^o\):\(2\)=\(15^o\)
Vì \(On\)là tia phân giác của góc \(zOy\)nên:\(\widehat{yOn}\)=\(90^o\):\(2\)=\(45^o\)
Vậy \(\widehat{mOn}\)=\(\widehat{nOy}\)+\(\widehat{mOy}\)=\(15^o\)+\(45^o\)=\(60^o\)
30 tháng 3 2017
mình lam đc lâu rồi nhưng dù sao thì cg cam on ban nha
LL
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
1
HN
21 tháng 6 2017
Bài 6:
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).
T
18 tháng 4 2019
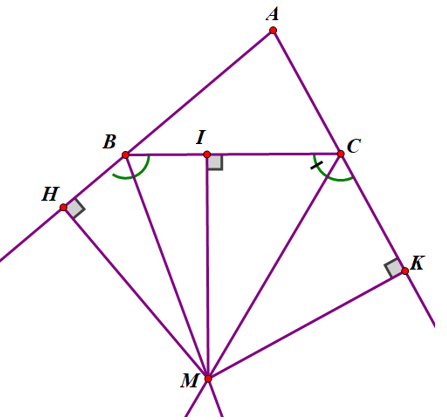
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
8 tháng 7 2019
Hình thì bạn tự vẽ nhé !!
Ta có : \(\widehat{CID}=115^o\)
Tổng 2 \(\widehat{ICD}=\widehat{IDC}=65^o\)
Ta tính tổng 2 \(\widehat{C}\)và \(\widehat{D}\)là : \(65^o.2=130^o\)
2 \(\widehat{A}\)và \(\widehat{B}\)là 230o
Ta chỉ thấy có \(\widehat{A}=140^o\)và \(\widehat{B}=90^o\) thì mới phù hợp
Vậy .................
a: Ta có: mn//xy
=>\(\widehat{mAB}=\widehat{ABy}\)(hai góc so le trong)
=>\(\widehat{mAB}=60^0\)
b:
Ta có: \(\widehat{yBc}+\widehat{yBA}=180^0\)(hai góc kề bù)
=>\(\widehat{yBc}=180^0-60^0=120^0\)
Bz là phân giác của góc yBc
=>\(\widehat{yBz}=\widehat{cBz}=\dfrac{\widehat{yBc}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{nAB}+\widehat{mAB}=180^0\)(hai góc kề bù)
=>\(\widehat{nAB}=180^0-60^0=120^0\)
At là phân giác của góc nAB
=>\(\widehat{nAt}=\widehat{tAB}=\dfrac{\widehat{nAB}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{ABz}=\widehat{ABy}+\widehat{yBz}=60^0+60^0=120^0\)
Ta có: \(\widehat{ABz}+\widehat{BAt}=120^0+60^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên At//Bz