Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vậy với điều kiện x ≠ 0 và x ≠ ± 1 thì biểu thức đã cho không phụ thuộc biến x.
bạn ơi cho mik hỏi sao x^2+2x+1/x -2x+2/x lại bàng x^2-1/x thế ak
Biểu thức xác định khi x 2 - 36 ≠ 0 , x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6 ≠ 0
x 2 - 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x 2 + 6 x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
Vậy biểu thức không phụ thuộc vào biến x.
Ta có
xác định khi x + 1
≠
0 và x – 1
≠
0 ⇒ x
≠
±
1
xác định khi x – 1 ≠ 0 và x2 – 1
≠
0 ⇒ x
≠
±
1
Vậy điều kiện để biểu thức xác định x ≠ ± 1
Ta có
Vậy với x ≠ ± 1 thì biểu thức đã cho không phụ thuộc vào x.
Biểu thức xác định khi x – 1 ≠ 0, x 2 - 2 x + 1 ≠ 0 và x 2 - 1 ≠ 0
x – 1 ≠ 0 ⇒ x ≠ 1
x 2 - 2 x + 1 ≠ 0 ⇒ x - 1 2 ≠ 0 ⇒ x ≠ 1
x 2 - 1 ≠ 0 ⇒ (x – 1)(x + 1) ≠ 0 ⇒ x ≠ -1 và x ≠ 1
Vậy biểu thức xác định với x ≠ -1 và x ≠ 1
Ta có:
Vậy biểu thức không phụ thuộc vào biến x.
Đa thức biểu thị kết quả thứ nhất: K = (x + 1)2
Đa thức biểu thị kết quả thứ hai: H = (x – 1)2
Đa thức biểu thị kết quả cuối cùng:
Q = K – H = (x + 1)2 - (x – 1)2
= (x+1).(x+1) - (x – 1). (x – 1)
= x.(x+1) + 1.(x+1) - x(x-1) + (-1). (x-1)
= x.x + x.1 + 1.x + 1.1 –[ x.x – x .1 + (-1).x + (-1) . (-1)]
= x2 + x + x + 1 – (x2 – x – x + 1)
= x2 + x + x + 1 – x2 + x + x – 1
= (x2 - x2 ) + (x+x+x+x) + (1- 1)
= 4x
Để tìm x, ta lấy kết quả cuối cùng chia cho 4
a) \(P=\left(\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}-\frac{2}{4-x}\right):\frac{\sqrt{x}+3}{\sqrt{x}-2}\left(ĐK:x\ge0;x\ne4\right)\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}-2+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(=\frac{x+2\sqrt{x}+\sqrt{x}}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}=\frac{\sqrt{x}}{\sqrt{x}+2}\)
b) Vì: \(\sqrt{x}+4>0,\forall x\inĐK\)
=> \(2\sqrt{x}+4>\sqrt{x}\)
=> \(\frac{\sqrt{x}}{2\sqrt{x}+4}< 0\)
=> \(\frac{\sqrt{x}}{\sqrt{x}+2}< 2\)
=>đpcm
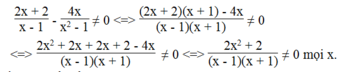
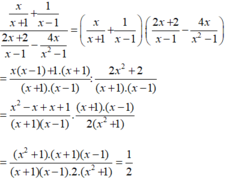
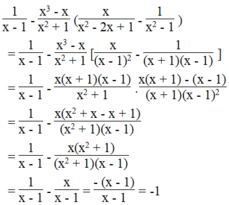
a: \(A=\dfrac{2x}{x+3}+\dfrac{x+1}{x-3}+\dfrac{3-11x}{9-x^2}\)
\(=\dfrac{2x}{x+3}+\dfrac{x+1}{x-3}+\dfrac{11x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x\left(x-3\right)+\left(x+1\right)\left(x+3\right)+11x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x^2-6x+x^2+4x+3+11x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x^2+9x}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x}{x-3}\)
b: Thay x=5 vào A, ta được:
\(A=\dfrac{3\cdot5}{5-3}=\dfrac{15}{2}\)