Cho hình bình hành ABCD. Hai đường thẳng đi qua tâm của hình bình hành chia nó thành bốn tứ giác có diện tích bằng nhau. Đường thẳng thứ nhất cắt BC tại E, đường thẳng thứ 2 cắt CD tại F. Chứng minh E chia cạnh BC và F chia cạnh CD theo cùng một tỉ số.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 2 2018
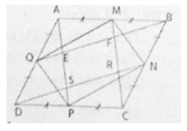
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2
CM
1 tháng 1 2017
Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành
27 tháng 11 2023
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔOAK và ΔOCH có
\(\widehat{OAK}=\widehat{OCH}\)(hai góc so le trong, AK//CH)
OA=OC
\(\widehat{AOK}=\widehat{COH}\)(hai góc đối đỉnh)
Do đó: ΔOAK=ΔOCH
=>OK=OH
=>O là trung điểm của KH
Xét ΔOAE và ΔOCF có
\(\widehat{EAO}=\widehat{FCO}\)(hai góc so le trong, AE//CF)
OA=OC
\(\widehat{AOE}=\widehat{COF}\)
Do đó: ΔOAE=ΔOCF
=>OE=OF
=>O là trung điểm của EF
Xét tứ giác EKFH có
O là trung điểm chung của EF và KH
=>EKFH là hình bình hành
29 tháng 8 2021
ABCD là hbh=> AD//BC=> góc DAC= góc ACB và AO=OC
Xét tam giác AOE và tam giác COF ta có
góc AOE = góc COF (2 góc đối xừng)
AO=OC
góc DAC= góc ACB
=> tam giác AOE = tam giác COF=> OE=OF
CHứng minh tương tự ta có tam giác AOK= tam giác COH=> OK=OH
Xét tứ giác EHFK có EH và FK là 2 đường chéo cắt nhau tại O
lại có OE=OF
OH=OK
=> EHFk là hình bình hành (do 2 đường chéo cắt nhau tại trung điểm mỗi đường)