Hình thang ABCD có AB//CD, \(\widehat{D}=60^o,\widehat{C}=30^o,AB=2cm,CD=6cm\). Tính đường cao của hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
23 tháng 8 2019
Kẻ BE // AD (E thuộc CD) ---> ^BEC = ^ADC = 60*
ABED là hình bình hành ---> DE = 2 ---> EC = 4
Tam giác BEC có ^BEC = 60*; ^BCE = 30* nên nó bằng nửa tam giác đều
---> BE = EC/2 = 2
Gọi BH là đường cao hình thang.
Tam giác BEH cũng là nửa tam giác đều (vì ^BEH = 60*; ^BHE = 90*)
---> EH = BE/2 = 1
---> BH^2 = BE^2 - EH^2 = 2^2 - 1 = 3 ---> BH =√ 3 (cm)
Trả lời : √3 cm.
MN
31 tháng 7 2020
Vì AB // CD nên \(\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^o}{2}=90^o\)
\(\Rightarrow\)Tứ giác ABCH có 3 góc vuông là hình chữ nhật
Ta có : \(DH=DC-HC\)
\(=DC-AB\) (Vì AB = HC)
\(=4-3\)
\(=1\left(cm\right)\)
Lại có : \(\hept{\begin{cases}\widehat{A}=3\widehat{D}\\\widehat{A}+\widehat{D}=180^o\left(slt\right)\end{cases}\Rightarrow}\hept{\begin{cases}\widehat{A}=135^o\\\widehat{D}=45^o\end{cases}}\)
\(\Rightarrow\)△AHD vuông tại H có ^ADH = 45o
\(\Rightarrow\)△AHD vuông cân tại H
\(\Rightarrow\)AH = DH
\(\Rightarrow\)AH = 1 (cm)
Vậy \(S_{ABCD}=\frac{\left(AB+CD\right)\cdot AH}{2}=\frac{\left(4+3\right)\cdot1}{2}=3,5\left(cm^2\right)\)
31 tháng 7 2020
Xét hình thang ABCD có \(AB//CD\)(gt) có:
\(\widehat{A}+\widehat{D}=180^0\)(trong cùng phía)
Mà \(\widehat{A}=3\widehat{D}\left(gt\right)\)
\(\Rightarrow3\widehat{D}+\widehat{D}=180^0\)
\(\Leftrightarrow4\widehat{D}=180^0\)
\(\Leftrightarrow\widehat{D}=45^0\)
\(\Rightarrow\widehat{A}=3.45^0=135^0\)
Ta có:\(AB//CD\left(gt\right)\)\(\Rightarrow\widehat{B}+\widehat{C}=180^0\)
Mà \(\widehat{B}=\widehat{C}\left(gt\right)\)\(\Rightarrow\widehat{B}+\widehat{B}=180^0\)
\(\Leftrightarrow2\widehat{B}=180^0\)
\(\Leftrightarrow\widehat{B}=90^0\Rightarrow\widehat{C}=90^0\)
Xét tứ giác ABCH có \(\widehat{B}=\widehat{C}=\widehat{H}=90^0\left(cmt\right)\)
\(\Rightarrow\)Tứ giác ABCH là hình chữ nhật (DHNB)
\(\Rightarrow AB=CH=3cm\)(t/c) \(\Rightarrow DH=CD-CH=4-3=1\left(cm\right)\)
Xét \(\Delta AHD\)có \(\widehat{H}=90^0,\widehat{D}=45^0\left(cmt\right)\)
\(\Rightarrow\Delta AHD\)vuông cân tại A (DHNB) \(\Rightarrow AH=DH=1cm\)(t/c)
Diện tích hình thang ABCD có:
\(S_{ABCD}=\frac{\left(AB+CD\right)\times AH}{2}=\frac{\left(3+4\right)\times1}{2}=3,5\left(cm^2\right)\)
Đáp số \(3,5cm^2\)
Học tốt
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2021
Kẻ đường cao BE ứng với CD \(\Rightarrow BE=4\left(cm\right)\)
Trong tam giác vuông BCE ta có:
\(\widehat{EBC}=90^0-\widehat{C}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{EBC}=\widehat{C}\Rightarrow\Delta BCE\) vuông cân tại E
\(\Rightarrow EC=BE=4\left(cm\right)\)
Tứ giác ABED là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AB=DE\)
Ta có:
\(AB+CD=10\left(cm\right)\)
\(\Leftrightarrow AB+DE+EC=10\)
\(\Leftrightarrow2AB+4=10\)
\(\Rightarrow AB=3\left(cm\right)\)
\(\Rightarrow DE=AB=3cm\Rightarrow CD=DE+EC=7\left(cm\right)\)
A
21 tháng 1 2021
Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2
21 tháng 1 2021
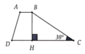
Kẻ BH \(\perp\) CD tại H
Xét tam giác BHC vuông tại H (BH \(\perp\) CD): \(\widehat{C}\) = 30o
\(\Rightarrow\) BH = \(\dfrac{1}{2}\)BC (Tính chất cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
hay BH = \(\dfrac{1}{2}\).8 = 4(cm)
Vì ABCD là hình thang (AB // CD)
\(\Rightarrow\) SABCD = \(\dfrac{1}{2}\)(AB + CD).BH = \(\dfrac{1}{2}\).(2 + 9).4 = 22 (cm2)
Chúc bn học tốt!
16 tháng 1 2020
Kẻ \(BE\perp CD\)
Xét \(\Delta BEC\)vuông tại E có :
\(\widehat{BEC}=90^o\) ( theo cách vẽ )
Mà \(\widehat{C}=45^o\)(gt)
\(\Rightarrow\Delta BEC\)vuông cân tại E
\(\Rightarrow BE=EC\)( tính chất tam giác vuông cân )
Hay \(BE\perp DC\)(1)
Vì \(\widehat{D}=90^o\left(gt\right)\)
\(\Rightarrow AD\perp DC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AD//BE\)( từ vuông góc đến song song )
Hình thang \(ABED\) có \(AD//BE\left(cmt\right)\)
\(\Rightarrow AB=DE\)( theo nhận xét của hình thang )
Mà \(AB=2cm\left(gt\right)\)
\(\Rightarrow AB=DE=2cm\)
Ta có \(EC=CD-BE\)
\(\Rightarrow EC=4-2\)
\(\Rightarrow EC=2cm\)
Mà BE = EC (cmt)
\(\Rightarrow BE=2cm\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}\left(AB+CD\right).BE=\frac{1}{2}.\left(2+4\right).2=\frac{1}{2}.6.2=6\left(cm^2\right)\)
Vậy \(S_{ABCD}=6\left(cm^2\right)\)
Chúc bạn học tốt !!!
BN
1
VS
14 tháng 7 2018
Kẻ BE // AD (E thuộc CD) ---> ^BEC = ^ADC = 60*
ABED là hình bình hành ---> DE = 2 ---> EC = 4
Tam giác BEC có ^BEC = 60*; ^BCE = 30* nên nó bằng nửa tam giác đều
---> BE = EC/2 = 2
Gọi BH là đường cao hình thang.
Tam giác BEH cũng là nửa tam giác đều (vì ^BEH = 60*; ^BHE = 90*)
---> EH = BE/2 = 1
---> BH^2 = BE^2 - EH^2 = 2^2 - 1 = 3 ---> BH =√ 3 (cm)
Học tốt ^-^