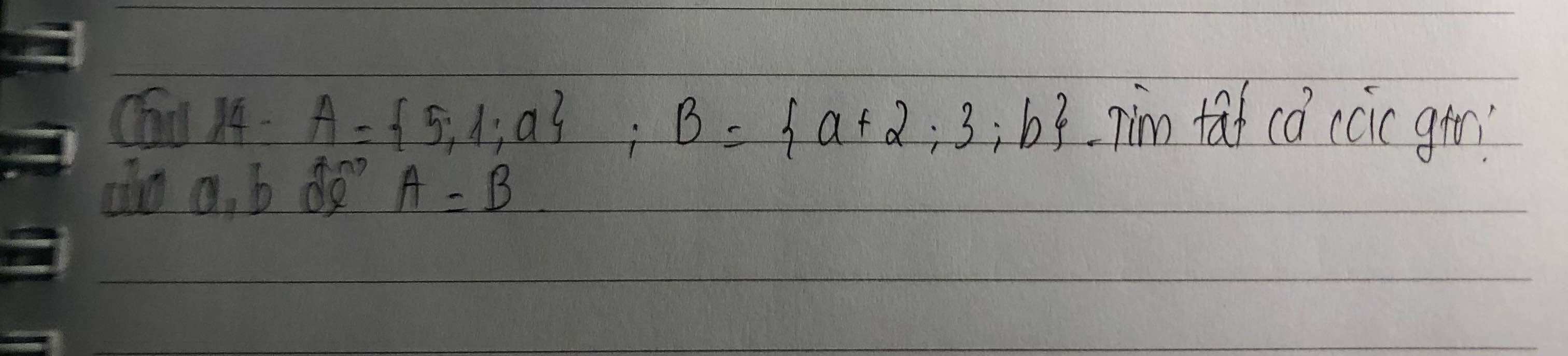Mọi ng ơi giúp em với ạ, em đang cần gấp ạ 😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
24 tháng 10 2021
c: include <bits/stdc++.h>
using namespace std;
long long a,b,c;
int main()
{
cin>>a>>b>>c;
cout<<max(a,max(b,c));
return 0;
}
23 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
long long n,i,x,nn;
int main()
{
cin>>n;
cin>>x;
nn=x;
for (i=1; i<n; i++)
{
cin>>x;
nn=min(nn,x);
}
cout<<nn;
return 0;
}
3 tháng 5 2016
Bài 1:a=b*\(\frac{m}{n}\)
Bài 2:b=a:\(\frac{3}{2}\)
Bài 3:cho hỏi tỉ số % hở
BA
28 tháng 12 2020
Input: dãy số nguyên gồm n số được nhập từ bạn phím
Output: số lớn nhất, bé nhất trong dãy
BA
28 tháng 12 2020
B1: nhập dãy số nguyên
B2: gán max:=a[1]; min:=a[1]
B3: nếu max<a[i] thì max:=a[i]; min>a[i] then min:=a[i]
B4: in kết quả ra màn hình
17 tháng 12 2020
1: Hoán đổi giá trị hai biến x và y
Chúng ta sẽ gán biến trung gian tam cho x, xong rồi gán biến trung gian tam đó cho y; rồi sau đó gán y ngược lại cho x, và xuất kết quả ra-đó chính là x và y sau khi hoán đổi cho nhau.
2: Tìm giá trị lớn nhất của dãy A
Chúng ta sẽ gán biến ln cho a[1], sau đó sẽ quét qua các phần tử trong mảng xem thử có phần tử nào lớn hơn ln thì gán ln cho phần tử đó. Sau cùng xuất ln ra, ta được số lớn nhất cần tìm.
9 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
long long a[10000],n,i,ln;
int main()
{
cin>>n;
ln=LLONG_MIN;
for (i=1; i<=n; i++)
{
cin>>a[i];
ln=max(ln,a[i]);
}
for (i=1; i<=n; i++)
if (ln==a[i]) cout<<i<<" ";
return 0;
}
10 tháng 12 2021
Chị có thể trình bày ra các bước liệt kê đc k chị.
Chẳng hạn như
B1: ...
B2: ...
B3: ...
31 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
double x,t;
int n,i;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
t=t+x;
}
cout<<"tong cac so la:"<<fixed<<setprecision(2)<<t<<endl;
cout<<"trung binh la:"<<fixed<<setprecision(2)<<t/(n*1.0);
return 0;
}
CM
31 tháng 7 2017
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
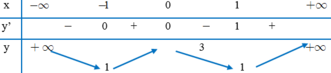
* Bước 3: Ta có bảng biến thiên sau:
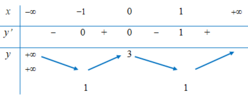
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
Nếu \(a\ne3\Rightarrow\) tập B có phần tử 3 nhưng tập A ko có \(\Rightarrow A\ne B\) (ko thỏa mãn)
\(\Rightarrow a=3\)
Khi đó \(A=\left\{5;1;3\right\}\) ; \(B=\left\{5;3;b\right\}\)
\(\Rightarrow b=1\)