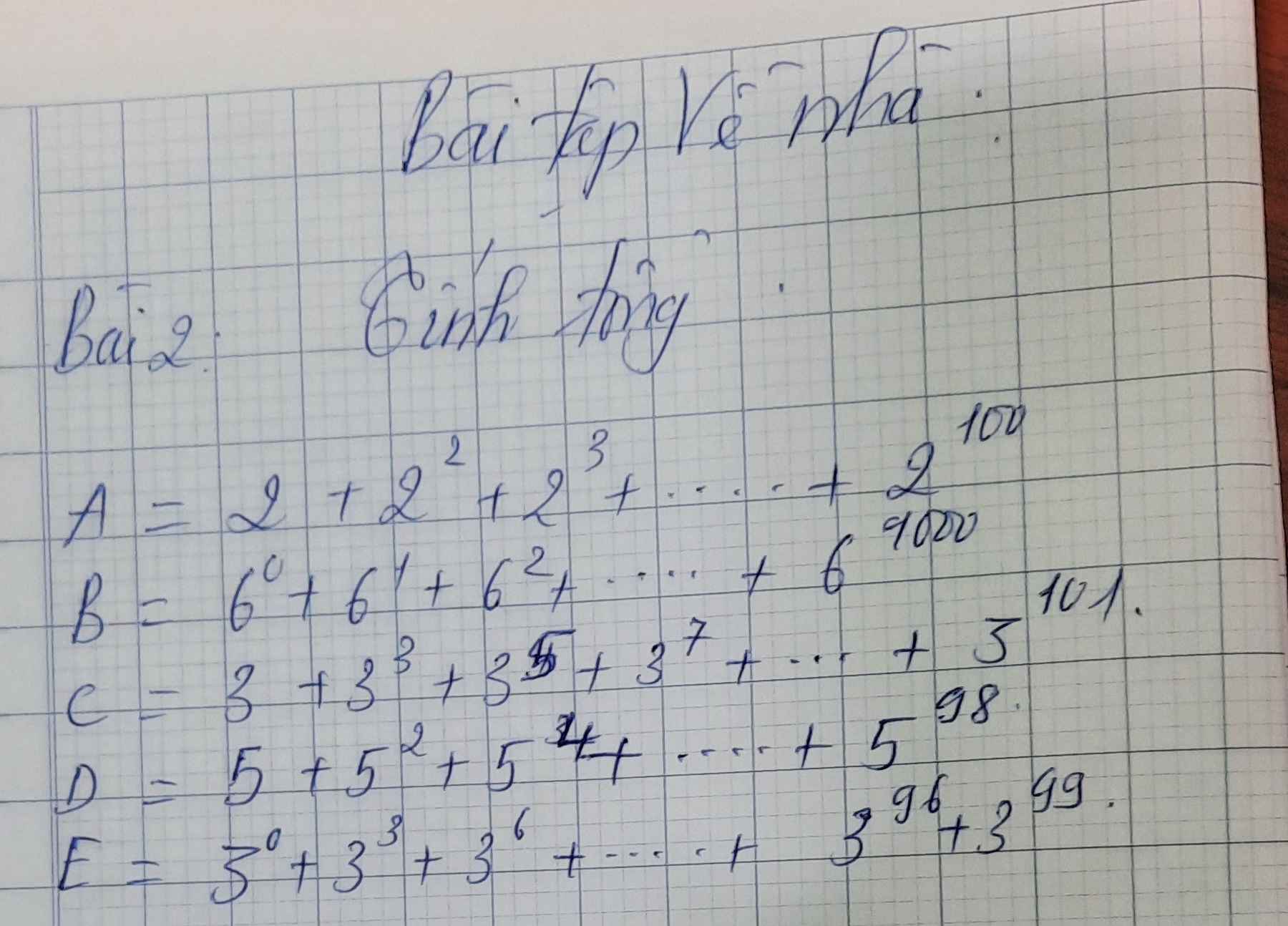 giúp với
giúp với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


uses crt;
var i,t,kt,j:integer;
begin
clrscr;
t:=0;
for i:=999 downto 100 do
begin
kt:=0;
for j:=2 to trunc(sqrt(i)) do
if i mod j=0 then kt:=1;
if kt=0 then t:=t+i;
end;
writeln('Tong cac so nguyen to trong day la: ',t);
readln;
end.

- Vì đề yêu cầu là các số lẻ liên tiếp nên phải là 1, 3, 5, .... nên khoảng cách giữa chúng sẽ là 2 .

a) Xác định bài toán
-Input: Dãy n số
-Output: Tổng các số dương, tổng các số âm
b) Mô tả thuật toán
-Bước 1: Nhập n và nhập dãy số
-Bước 2: t1←0; t2←0; i←1;
-Bước 3: Nếu a[i]>0 thì t1←t1+a[i]
nếu a[i]<0 thì t2←t2+a[i];
-Bước 4: i←i+1;
-Bước 5: Nếu i<=n thì quay lại bước 3
-Bước 6: Xuất t1,t2
-Bước 7: Kết thúc

Bài 1:
program in_phan_tu;
uses crt;
var n,i:longint;
a:array[1..100] of longint;
begin
clrscr;
write('nhap so n:');readln(n);
for i:=1 to n do
begin
write('nhap phan tu a[',i,']:');readln(a[i]);
end;
for i:=1 to n do
write(a[i]:3);
readln;
end.
Bài 2:
program tong_phan_tu;
uses crt;
var n,i,tong:longint;
a:array[1..100] of longint;
begin
clrscr;
write('nhap so n:');readln(n);
for i:=1 to n do
begin
write('nhap phan tu a[',i,']:');readln(a[i]);
end;
tong:=0;
for i:=1 to n do
tong:=tong+a[i];
writeln('tong cua day la:');
readln;
end.
Bài 3:
program tong_phan_tu_chan;
uses crt;
var n,i,tong:longint;
a:array[1..100] of longint;
begin
clrscr;
write('nhap so n:');readln(n);
for i:=1 to n do
begin
write('nhap phan tu a[',i,']:');readln(a[i]);
end;
tong:=0;
for i:=1 to n do
if a[i] mod 2=0 then tong:=tong+a[i];
writeln('tong cua day la:');
readln;
end.
Câu 1:
uses crt;
var a:array[1..100]of integer;
i,n:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(a[i]:4);
readln;
end.
\(A=2+2^2+...+2^{100}\\ 2A=2^2+2^3+...+2^{101}\\ 2A-A=\left(2^2+2^3+...+2^{101}\right)-\left(2+2^2+...+2^{100}\right)\\ A=2^{101}-2\\ B=6^0+6^1+6^2+...+6^{1000}\\ 6B=6+6^2+...+6^{1001}\\ 6B-B=\left(6+6^2+...+6^{1001}\right)-\left(1+6+...+6^{1000}\right)\\ 5B=6^{1001}-1\\ B=\dfrac{6^{1001}-1}{5}\\ C=3+3^3+3^5+...+3^{101}\\ 3^2C=3^3+3^5+3^7+...+3^{103}\\ 9C-C=\left(3^3+3^5+3^7+...+3^{103}\right)-\left(3+3^3+3^5+...+3^{101}\right)\\ 8C=3^{103}-3\\ C=\dfrac{3^{103}-3}{8}\)
\(D=5+5^2+5^4+...+5^{98}\\ 5^2D=5^3+5^4+5^6+...+5^{100}\\ 25D-D=\left(5^3+5^4+5^6+....+5^{100}\right)-\left(5+5^2+5^4+...+5^{98}\right)\\ 24D=5^{100}+5^3-5-5^2\\ 24D=5^{100}+125-5-25\\ 24D=5^{100}+95\\ D=\dfrac{5^{100}+95}{24}\\ E=3^0+3^3+3^6+...+3^{96}+3^{99}\\ E=1+3^3+...+3^{99}\\ 3^3E=3^3+3^6+...+3^{102}\\ 27E-E=\left(3^3+3^6+...+3^{102}\right)-\left(1+3^3+...+3^{99}\right)\\ 26E=3^{102}-1\\ E=\dfrac{3^{102}-1}{6}\)