cứu bài này vs khó qué, vẽ hình giúp mình luôn nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VX
2
Những câu hỏi liên quan
15 tháng 10 2017
bạn vẽ hình nha mk ko biết vẽ sorry
Áp dung định lí pytago vào tam giác ABC vuông tại A đường cao AH ta có:
\(AB^2+AC^2=BC^2\)
hay \(4^2+3^2=BC^2\)
\(\Rightarrow BC^2=16+9\)
\(\Rightarrow BC^2=25\)
\(\Rightarrow BC=5\left(cm\right)\)
Áp dụng hệ thức giữa cạnh và đường vào tam giác vuông \(ABC\)vuông tại \(A\) đường cao \(AH\) ta có:
+ \(AB^2=BH.BC\)
hay \(4^2=HB.5\)
\(\Rightarrow HB=16:5\)
\(\Rightarrow HB=3,2\left(cm\right)\)
+ \(AC^2=HC.BC\)
hay \(3^2=HC.5\)
\(\Rightarrow HC=9:5\)
\(\Rightarrow HC=1,8\left(cm\right)\)
vậy \(HB=3,2cm\)
\(HC=1,8cm\)
CM
3 tháng 10 2018
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H
⇒ CH =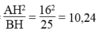 
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ AB = 
≈ 29,68
A C 2 = H C . B C
⇒ AC = 
≈ 18,99
CM
29 tháng 6 2017
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ BC = 
= 24
CH = BC – BH = 24 – 6 = 18
Theo hệ thức liên hệ giữa các cạnh góc vuông và hình chiếu, ta có:
A
C
2
=
H
C
.
B
C
⇒ AC = 
≈ 20,78
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
A
H
2
=
H
B
.
B
C
⇒ AH = 
LH
0
15 tháng 7 2016
Lm s để viết đc chữ màu xanh mà nhấp chuột vào là vào trang đó đc z bn??? Chỉ mk vs
24 tháng 7 2018
a) Áp dụng Pi-ta-go cho \(\Delta AHB\)vuông tại H ta có :
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow16^2+25^2=AB^2\)
\(\Leftrightarrow AB=\sqrt{881}\left(cm\right)\)
Áp dụng hệ thức về đường cao trong tam giác vuông ta có :
\(AH^2=HB\times HC\)
\(\Leftrightarrow16^2=25\times HC\)
\(\Leftrightarrow HC=10,24\left(cm\right)\)
Ta có : \(BC=CH+BH=10,24+25=35,24\left(cm\right)\)
Áp dụng Pi-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=35,24^2-\sqrt{881}^2\)
\(\Leftrightarrow AC=360,8576\left(cm\right)\)
b) Áp dụng Pi-ta-go cho \(\Delta AHB\)vuông tại H ta có :
\(AH^2=AB^2-HB^2\)
\(\Leftrightarrow AH^2=12^2-6^2\)
\(\Leftrightarrow AH=6\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức trong tam giác ta có :
\(AH^2=CH\times HB\)
\(\Leftrightarrow CH=18\left(cm\right)\)
Ta có : \(BC=CH+BH=18+6=24\left(cm\right)\)
Áp dụng Pi-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=24^2-12^2\)
\(\Leftrightarrow AC=12\sqrt{3}\left(cm\right)\)
Vậy ...
L
25 tháng 11 2020
a)
- Áp dụng định lí Py - ta - go cho tam giác vuông HAB ( \(\widehat{H}=90^o\))
\(AB^2=BH^2+AH^2\)
\(=25^2+16^2\)
\(=625+256=881\)
\(\Rightarrow AB=\sqrt{881}\approx29,6\left(cm\right)\)
- Áp dụng hệ thức lượng trong tam giác ABC ( \(\widehat{A}=90^o\)) , đường cao AH , ta có :
+) AH2 = HB . HC
\(16^2=25.HC\)
\(HC=\frac{16^2}{25}=\frac{256}{25}=10,24\left(cm\right)\)
+) BC = BH + HC = 25 + 10,24 = 35,24 ( cm )
\(+)AC^2=HC.BC=10,24.35,24\approx360,86\left(cm\right)\)
\(\Rightarrow AC=\sqrt{360,86}\approx18,9cm\)
Vậy : ..................
b)
- Áp dụng định lí Py - ta - go cho tam giác vuông AHB ( \(\widehat{H}=90^o\)) , ta có :
AB2 = BH2 + AH2
122 = 62 + AH2
AH2 = 122 - 62
= 144 - 366 = 108 ( cm )
\(\Rightarrow AH=\sqrt{108}\approx10,39\left(cm\right)\)
- Áp dụng hệ thức lượng cho tam giác ABC ( \(\widehat{A}=90^o\)) , đường cao AH , ta có :
\(+)AH^2=BH.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{10,39^2}{6}=17,99\left(cm\right)\)
\(+)BC=BH+HC=6+17,99=23,99\left(cm\right)\)
\(+)AC^2=BC.HC=23,99.17,99=431,58\left(cm\right)\)
\(+)AC=\sqrt{431,58}\approx20,77\left(cm\right)\)
Vậy : ....................
8 tháng 1 2021
a. - Áp dụng hệ thức về cạnh và đường cao trong Δ vuông vào ΔABC vuông tại A ta có :
\(AH=\sqrt{CH.BH}=\sqrt{2.4}=2\sqrt{2}\) ( Đ.lý 2 )
- Áp dụng đ.lý Pytago vào \(\Delta AHB\perp H\) ta có :
\(AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{2}\right)^2+4^2}=2\sqrt{6}\)
- \(BC=2+4=6\)
- Theo đ.lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-\left(2\sqrt{6}\right)^2}=2\sqrt{3}\)
b. - Áp dụng hệ thức...trong Δ vuông ABC ta có :
+ \(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=24\) ( Đ.lý 1 )
\(\Rightarrow CH=BC-BH=24-6=18\)
+ \(AH=\sqrt{BH.CH}=\sqrt{6.18}=6\sqrt{3}\) ( Đ.'ý 2 )
- Theo đ.lý Pytago ta có :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{24^2-12^2}=12\sqrt{3}\)
8 tháng 1 2021
a, BC = BH+HC
*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)
*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)
*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)
b,Theo định lý pytago ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)
*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)
*\(CH=BC-BH=24-6=18\)
\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)
22 tháng 11 2016
Bài 4:
Gọi M là giao điểm của EF với BC, N là giao điểm của DF với AB, ta có:
Ta có: DF vuông góc với AH
BC vuông góc với AH
DF song song với BC (hay BM) (2 góc trong cùng phía)
Mà là góc ngoài của nên
AB song song với MF (hay EF) (vì có 2 góc đồng vị bằng nhau) (1)
(2 góc so le trong)
Xét và có:
AH = DE (vì AD +DH = DH + HE)
(ch/minh trên)
(cạnh góc vuông - góc nhọn) DF = BH (2 cạnh tương ứng)
Xét và có:
HE = AD (gt)
BH = DF (ch/minh trên)
(2 cạnh góc vuông) (2 góc tương ứng)
BE song song với AF (hay AC) (vì có 2 góc so le trong bằng nhau) (2)
Mặt khác: BA vuông góc với AC (3)
Từ (1), (2) và (3) suy ra: BE vuông góc với EF (đpcm)
a: Ta có: \(\widehat{HAC}+\widehat{ACB}=90^0\)(ΔAHC vuông tại H)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{HAC}=\widehat{ABC}\)
b: Ta có: \(\widehat{CAK}+\widehat{BAK}=\widehat{BAC}=90^0\)
\(\widehat{CKA}+\widehat{HAK}=90^0\)(ΔHAK vuông tại H)
mà \(\widehat{BAK}=\widehat{HAK}\)(AK là phân giác của góc HAB)
nên \(\widehat{CAK}=\widehat{CKA}\)
c: Xét ΔCAK có \(\widehat{CAK}=\widehat{CKA}\)
nên ΔCAK cân tại C
ΔCAK cân tại C
mà CP là đường phân giác
nên CP\(\perp\)AK