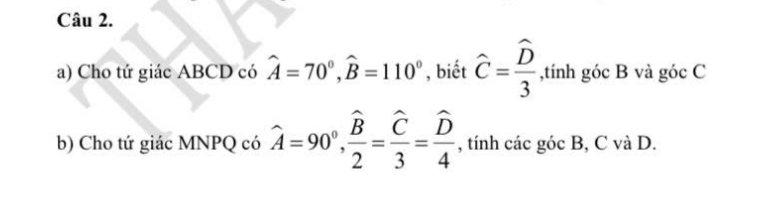
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{C}+\widehat{D}=360^0-110^0-70^0=180^0\)
=>\(\dfrac{1}{3}\cdot\widehat{D}+\widehat{D}=180^0\)
=>\(\dfrac{4}{3}\cdot\widehat{D}=180^0\)
=>\(\widehat{D}=135^0\)
\(\widehat{C}=\dfrac{1}{3}\cdot135^0=45^0\)
b:
Sửa đề: Cho tứ giác ABCD.
Đặt \(\widehat{B}=x;\widehat{C}=y;\widehat{D}=z\)
\(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
=>\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(x+y+z=360^0-90^0=270^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{270}{9}=30^0\)
=>\(x=2\cdot30^0=60^0;y=3\cdot30^0=90^0;z=4\cdot30^0=120^0\)
Vậy: \(\widehat{B}=x=60^0;\widehat{C}=y=90^0;\widehat{D}=z=120^0\)