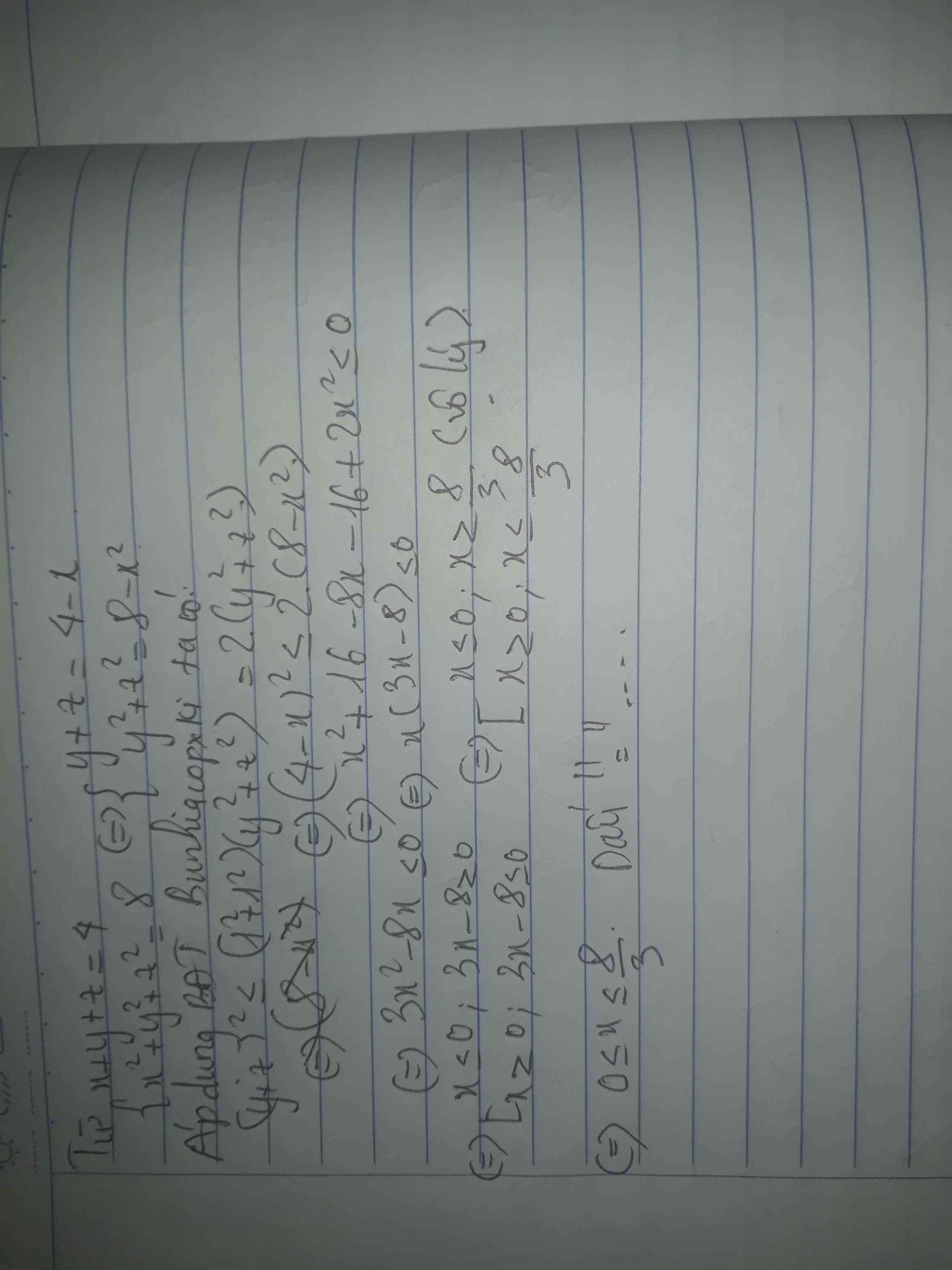tìm x,y thuộc Z tm x(x^2+x+1)=4y(y+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{y+1}{4x^2+1}=1-\frac{4x^2-y}{4x^2+1}\ge1-\frac{4x^2-y}{2\sqrt{4x^2.1}}=1+\frac{y}{4x}-x;\)
Tương tự ta được \(\frac{1+z}{4y^2+1}\ge1+\frac{z}{4y}-y\); \(\frac{1+x}{4z^2+1}\ge1+\frac{x}{4z}-z\)
cộng 3 bất đăng thức trên ta được p \(\ge3+\frac{1}{4}\left(\frac{y}{x}+\frac{z}{y}+\frac{x}{z}\right)-\left(x+y+z\right)=\frac{3}{2}+\frac{1}{4}\left(\frac{y}{x}+\frac{z}{y}+\frac{x}{z}\right)\ge\)\(\frac{3}{2}+\frac{1}{4}.3\sqrt[3]{\frac{y}{x}.\frac{z}{y}.\frac{x}{z}}=\frac{9}{4}\)
p min khi x=y=z = 1/2


\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)



x(x² + x + 1) = 4y(y + 1)
<=> (x + 1)(x² + 1) = (2y + 1)²
Dễ dàng thấy là: x + 1 và x² + 1 nguyên tố cùng nhau nên x + 1 và x² + 1 là 2 số chính phương.
=> x²; x² + 1 là 2 số chính phương liên tiếp
=> x = 0; y = 0 hoặc y = - 1

c/
\(\left(4y+1\right)\left(8-x\right)=20=1.20=5.4\)
-Nhận xét: 4y+1 là số chia 4 dư 1 nên ta có các trường hợp sau:
\(+4y+1=1\text{ và }8-x=20\Leftrightarrow\left(x;y\right)=\left(-12;0\right)\)
\(+4y+1=5\text{ và }8-x=4\Leftrightarrow\left(x;y\right)=\left(4;1\right)\)
Kết luận: \(\left(x;y\right)=\left(-12;0\right);\left(4;1\right)\)
Cách làm tương tự, đối với các câu a, b, ta chỉ thêm một bước là phân tích 1 vế thành nhân tử, 1 vế là số nguyên.
\(\text{a) }xy=x-y\Leftrightarrow\left(x+1\right)\left(y-1\right)=-1\)
\(\text{b) }x\left(y+2\right)+y=1\Leftrightarrow\left(x+1\right)\left(y+2\right)=3\)
minh ko biet lam bai nay nhung minh biet lam bai khac