giải
2x^2-6x+1=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có \(a = 3 > 0\) và tam thức bậc hai \(f\left( x \right) = 3{x^2} - 2x + 4\) có \(\Delta ' = {1^2} - 3.4 = - 11 < 0\)
=> \(f\left( x \right) = 3{x^2} - 2x + 4\) vô nghiệm.
=> \(3{x^2} - 2x + 4 > 0\forall x \in \mathbb{R}\)
b) Ta có: \(a = - 1 < 0\) và \(\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0\)
=> \(f\left( x \right) = - {x^2} + 6x - 9\) có nghiệm duy nhất \(x = 3\).
=> \( - {x^2} + 6x - 9 < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}\)

3:
a: u+v=14 và uv=40
=>u,v là nghiệm của pt là x^2-14x+40=0
=>x=4 hoặc x=10
=>(u,v)=(4;10) hoặc (u,v)=(10;4)
b: u+v=-7 và uv=12
=>u,v là các nghiệm của pt:
x^2+7x+12=0
=>x=-3 hoặc x=-4
=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)
c; u+v=-5 và uv=-24
=>u,v là các nghiệm của phương trình:
x^2+5x-24=0
=>x=-8 hoặc x=3
=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)


Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1


a) Ta có đồ thị:
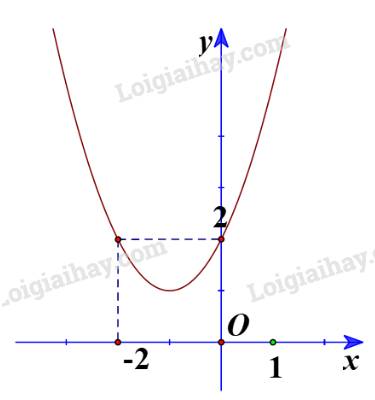
Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).
Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).
b) Ta có đồ thị:
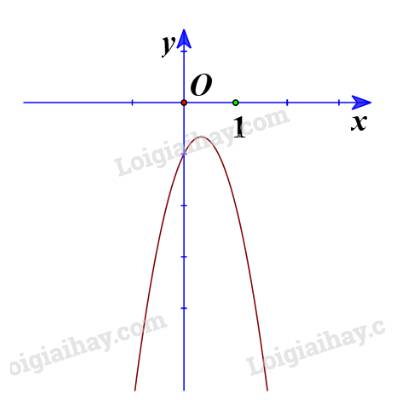
Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y = - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).

a: Khi m=1 thì phương trình sẽ là x^2-2x-1=0
=>x^2-2x+1-2=0
=>(x-1)^2=2
=>\(x=\pm\sqrt{2}+1\)
b: Δ=(-2)^2-4*1*(-m^2)=4m^2+4>=4>0
=>Phương trình luôn có hai nghiệm phân biệt

a) 2x2 – 7x + 3 = 0 có a = 2, b = -7, c = 3
∆ = (-7)2 – 4 . 2 . 3 = 49 – 24 = 25, \(\sqrt{\text{∆}}\) = 5
x1 = \(\dfrac{-\left(-7\right)-5}{2.2}\) = \(\dfrac{2}{4}\) = \(\dfrac{1}{2}\), x2 =\(\dfrac{-\left(-7\right)+5}{2.2}=\dfrac{12}{4}=3\)
b) 6x2 + x + 5 = 0 có a = 6, b = 1, c = 5
∆ = 12 - 4 . 6 . 5 = -119: Phương trình vô nghiệm
c) 6x2 + x – 5 = 0 có a = 6, b = 5, c = -5
∆ = 12 - 4 . 6 . (-5) = 121, \(\sqrt{\text{∆}}\) = 11
x1 = \(\dfrac{-5-1}{2.3}\) = -1; x2 = \(\dfrac{-1+11}{2.6}\) =
d) 3x2 + 5x + 2 = 0 có a = 3, b = 5, c = 2
∆ = 52 – 4 . 3 . 2 = 25 - 24 = 1, \(\sqrt{\text{∆}}\) = 1
X1 = \(\dfrac{-5-1}{2.3}\) = -1, x2 = \(\dfrac{-5+1}{2.3}\) = \(\dfrac{-2}{3}\)
e) y2 – 8y + 16 = 0 có a = 1, b = -8, c = 16
∆ = (-8)2 – 4 . 1. 16 = 0
y1 = y2 = \(-\dfrac{-8}{2.1}\) = 4
f) 16z2 + 24z + 9 = 0 có a = 16, b = 24, c = 9
∆ = 242 – 4 . 16 . 9 = 0
z1 = z2 = \(\dfrac{-24}{2.16}\) = \(\dfrac{3}{4}\)
\(2x^2-6x+1=0\)
\(\Leftrightarrow4x^2-12x+2=0\)
\(\Leftrightarrow\left(2x\right)^2-2.2x.3+9=7\)
\(\Leftrightarrow\left(2x-3\right)^2=7\)
\(\Leftrightarrow2x-3=\pm\sqrt{7}\)
\(\Leftrightarrow2x=\pm\sqrt{7}+3\)
\(\Leftrightarrow x=\dfrac{\pm\sqrt{7}+3}{2}\)
Vậy ...
`2x^2 - 6x + 1 = 0`
`Δ' = \(\left(\dfrac{b}{2}\right)^2-ac\) = 3^2 - 2.1 = 7 > 0`
=> Phương trình có 2 nghiệm phân biệt
\(\left[{}\begin{matrix}x=\dfrac{-\dfrac{b}{2}+\sqrt{\Delta}}{2}=\dfrac{3+\sqrt{7}}{2}\\x=\dfrac{-\dfrac{b}{2}-\sqrt{\Delta}}{2}=\dfrac{3-\sqrt{7}}{2}\end{matrix}\right.\)
Vậy ....