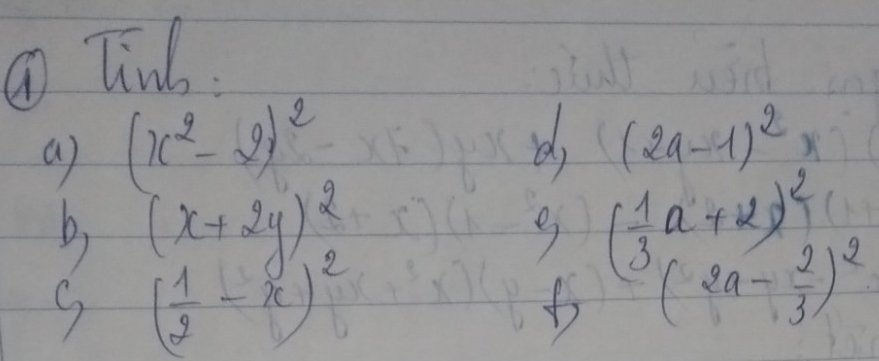
Giúp mình trong ngày hôm nay nhé. Mình cần kết quả gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TQ
2
TH
3
PT
2
22 tháng 2 2016
BÀI TOÁN DÂN SỐ
(Thái An)
I. KIẾN THỨC CƠ BẢN
1. Về vấn đề nêu trong văn bản:
Viết về hiểm hoạ của việc gia tăng dân số quá nhanh - một đề tài vừa khó vừa khô khan, tác giả đã chọn cách vào đề thật hấp dẫn, vừa thực tế, vừa giàu sức thuyết phục. Từ câu chuyện nhà giàu kén rể đến 64 ô bàn cờ với một lượng tóc "nhiều đến mức có thể phủ khắp bề mặt Trái Đất", bạn đọc dễ dàng hình dung về sự gia tăng dân số chóng mặt với tốc độ sinh sản như hiện nay.
2. Về cấu trúc và giá trị nội dung của văn bản:
a) Đề cập về một vấn đề bức xúc trong đời sống xã hội, văn bản Bài toán dân số được cấu trúc thành ba phần: Phần mở bài (từ đầu cho đến "sáng mắt ra"...), tác giả nêu ra vấn đề: bài toán dân số và kế hoạch hoá gia đình đã được đặt ra từ thời cổ đại; Phần thân bài (từ "Đó là câu chuyện từ bài toán cổ..." cho đến "...sang ô thứ 31 của bàn cờ"), tác giả làm rõ vấn đề đã được nêu ra: Tốc độ gia tăng nhanh chóng của dân số thế giới và Phần kết bài (từ "Đừng để cho..." đến hết): kêu gọi loài người cần kiềm chế tốc độ gia tăng dân số.
b) Trước hết, bài toán cổ và ý nghĩa về sự gia tăng nhanh chóng của số lượng: ô đầu tiên của bàn cờ chỉ là một hạt thóc, nếu gia tăng theo cấp số nhân thì đến hết 64 ô. Tốc độ gia tăng thực sự rất lớn ngoài sức tưởng tượng.
Thứ hai, sự gia tăng dân số của thế giới giống như lượng thóc tăng lên trong các ô bàn cờ. Lịch sử loài người tính đến năm 1995 đã là 5,63 tỉ người, nằm ở khoảng ô thứ ba mươi của bàn cờ trong bài toán cổ.
Thứ ba, để mỗi gia đình chỉ sinh hai con là điều rất khó thực hiện, vì trên thực tế, tỉ lệ phổ biến là phụ nữ sinh hơn hai con. Trong khi nếu đúng là mỗi gia đình chỉ sinh hai con thì chúng ta đang "mon men sang ô thứ 31 của bàn cờ".
c) Về cách thức thể hiện, với việc sử dụng câu chuyện kén rể của nhà thông thái, tác giả đã làm nổi bật vấn đề tốc độ gia tăng dân số; đồng thời làm tăng sức hấp dẫn cho bài viết. Mượn xưa để nói nay, sự giống nhau giữa số thóc tăng theo cấp số nhân với công bội hai và tình trạng bùng nổ dân số cả khi mỗi gia đình chỉ sinh hai con đã cho người đọc hình dung được một cách cụ thể về tốc độ gia tăng dân số. Tốc độ gia tăng nhanh đến mức bùng nổ được cảnh báo bằng hình ảnh một lượng thóc khổng lồ "có thể phủ kín bề mặt Trái Đất"...
c) Vì chính cuộc sống của chúng ta, hãy nhận thức đầy đủ về vấn đề dân số, cùng có trách nhiệm trong việc hạn chế sự gia tăng dân số. Đây chính là điều mà tác giả của bài viết mong muốn ở người đọc.
II. RÈN LUYỆN KĨ NĂNG
Văn bản ngắn gọn, trong đó các con số nói lên được nhiều điều. Cần đọc to, rõ ràng các con số để làm tăng thêm sức thuyết phục cho các lập luận của tác giả.
15 tháng 12 2017
Soạn bài: Bài toán dân số
Hướng dẫn soạn bài
Tóm tắt :
Bài toán dân số là một vấn đề không mới. Tác giả nêu câu chuyện kén rể của nhà thông thái từ một bài toán cổ trên 1 bàn cờ tướng 64 ô. Theo đó thì thừ khai thiên lập địa đến năm 1995, dân số thế giới đạt đến ô thứ 30 với điều kiện mỗi gia đình chỉ có 2 con. Trong thực tế 1 phụ nữ có thể sinh nhiều con. Tính theo bài toán cổ thì số dân đã mon men sang ô thứ 34 của bàn cờ. Cuối cùng tác giả báo động về con đường “tồn tại hay không tồn tại”.
Bố cục :
- Phần 1 (từ đầu … sáng mắt ra) : Bài toán dân số đặt ra từ thời cổ đại.
- Phần 2 (tiếp … ô thứ 31 của bàn cờ) : Sự tăng nhanh khủng khiếp của dân số.
+ Luận điểm 1 (Đó là câu… nhường nào) : Câu chuyện kén rể của nhà thông thái.
+ Luận điểm 2 (bây giờ … không quá 5%) : Sự phát triển của dân số thế giới.
+ Luận điểm 3 (trong thực tế … 34 của bàn cờ): tỉ lệ sinh của phụ nữ Á và Phi.
- Phần 3 (còn lại) : kêu gọi loài người hạn chế gia tăng dân số.
Câu 1 (trang 131 sgk Ngữ Văn 8 Tập 1): (bố cục như đã chia phần trên)
Câu 2 (trang 131 sgk Ngữ Văn 8 Tập 1):
- Vấn đề chính tác giả muốn đặt ra : sự gia tăng dân số thế giới tốc độ chóng mặt, con người cần hạn chế sự gia tăng dân số để tồn tại.
- Điều làm tác giả sáng mắt ra là sự gia tăng dân số trong thời buổi nay đã được đặt trong một bài toán cổ đại.
Câu 3 (trang 131 sgk Ngữ Văn 8 Tập 1):
Câu chuyện kén rể của nhà thông thái làm nổi bật vấn đề gia tăng dân số, sự liên tưởng đến số thóc với dân số thật bất ngờ, thú vị, tạo nên hình dung cụ thể.
Câu 4 (trang 132 sgk Ngữ Văn 8 Tập 1):
- Việc đưa ra những con số về tỉ lệ sinh con là bằng chứng rõ ràng cho thấy tỉ lệ sinh của phụ nữ Á, Phi vô cùng mạnh.
- Các nước thuộc châu Phi có Nê-pan, Ru-an-đa, Tan-za-ni-a, Ma-đa-gát-xca. Các nước Việt Nam, Ấn Độ thuộc châu Á. Hai châu lục này có tỉ lệ các nước kém phát triển cao, nghèo, và tỉ lệ gia tăng dân số mạnh.
Câu 5 (trang 132 sgk Ngữ Văn 8 Tập 1):
Văn bản này đưa đến cho chúng ta hiểu biết về tình hình gia tăng dân số đáng báo động trên thế giới và Việt Nam, để từ đó chúng ta có hành động thiết thực.
Luyện tậpCâu 1 (trang 132 sgk Ngữ Văn 8 Tập 1):
Con đường tốt nhất để hạn chế sự gia tăng dân số là đẩy mạnh giáo dục, đặc biệt là giáo dục phụ nữ.
Câu 2 (trang 132 sgk Ngữ Văn 8 Tập 1):
Sự gia tăng dân số có tầm quan trọng to lớn với tương lai nhân loại, nhất là với các dân tộc còn nghèo nàn, lạc hậu vì :
- Dân số tăng kèm theo nhu cầu kinh tế để nuôi dạy con cái.
- Gia đình đông con dễ dẫn đến sự giáo dục, chăm sóc thiếu chu đáo, thất học.
- Đất chật người đông, đời sống con người càng thêm khó khăn.
Câu 3 (trang 132 sgk Ngữ Văn 8 Tập 1):
Dân số tăng mỗi năm (từ năm 2000 đến 2010) là 77 258 877. Vậy từ năm 2000 – 2003, sau 3 năm dân số sẽ tăng 77 258 877 x 3 = 231 776 631.
Dân số Việt Nam theo số liệu thống kê vào năm 2016 là 94 104 871 người
⇒ gấp gần 2,5 lần so với Việt Nam.
YU
1
VC
0
TV
1
9 tháng 9 2017
A.Lý thuyết về dấu tam thức bậc hai
1. Tam thức bậc hai (một ẩn) là đa thức có dạng f(x) = ax2 + bx + c trong đó x là biến a, b, c là các số đã cho, với a ≠ 0.
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x = , với mọi x ≠
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
2. Bất phương trình bậc hai một ẩn.
Là mệnh đề chứa một biến có một trong các dạng:
ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ax2 + bx + c ≤ 0 trong đó vế trái là một tam thức bậc hai.
Để giải bất phương trình bậc hai một ẩn ta dùng định lí về dấu của tam thức bậc hai.
AY
20 tháng 2 2018
Ta có : Mai ăn 3/8 cái bánh, khi quy đồng ra thì Mai ăn 15/40 cái bánh. Hoa ăn 2/5 cái bánh, khi quy đồng ra thì Hoa ăn 16/40 cái bánh.
So sánh : 15/40 < 16/40. Tức: 3/8 < 2/5
Vậy: Hoa ăn nhiều bánh hơn Mai
\(a.\left(x^2-2\right)^2=\left(x^2\right)^2-2\cdot x^2\cdot2+2^2=x^4-4x^2+4\\ b.\left(x+2y\right)^2=x^2+2\cdot x\cdot2y+\left(2y\right)^2=x^2+4xy+4y^2\\ c.\left(\dfrac{1}{2}-x\right)^2=\left(\dfrac{1}{2}\right)^2-2\cdot x\cdot\dfrac{1}{2}+x^2=\dfrac{1}{4}-x+x^2\\ d.\left(2a-1\right)^2=\left(2a\right)^2-2\cdot2a\cdot1+1^2=4a^2-4a+1\\ e.\left(\dfrac{1}{3}a+2\right)^2=\left(\dfrac{1}{3}a\right)^2+2\cdot\dfrac{1}{3}a\cdot2+2^2=\dfrac{1}{9}a^2+\dfrac{4}{3}a+4\\ f.\left(2a-\dfrac{2}{3}\right)^2=\left(2a\right)^2-2\cdot2a\cdot\dfrac{2}{3}+\left(\dfrac{2}{3}\right)^2=4a^2-\dfrac{8}{3}a+\dfrac{4}{9}\)