mọi người ơi giúp em vớiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
18 tháng 4 2019
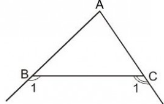
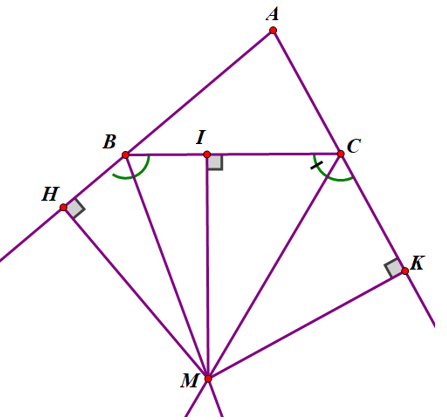
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
LL
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
1
HN
21 tháng 6 2017
Bài 6:
A P M N Q 33 o
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).
NQ
28 tháng 4 2016
Cho góc AOB bằng 135 độ,vẽ tia OC nằm trong góc sao cho góc BOC gấp 2 lần góc AOB.
a, Tính mỗi góc
b,Gọi tia OD là tia đối của tia OB. CMR : OA là tia phân giác của góc DOC
30 tháng 4 2016
cho tg ABC, AD là phân giác, góc  vuông tính góc ADB và ADC, so sánh 2 góc đó
MC
Cho hình vẽ
2
14 tháng 12 2016
Hình thiếu dữ kiện nên vẽ lại nhé!!
B C A D M
Gọi M là giao điểm của BC và AD
Xét tam giác ABM và tam giác DBM có:
AM = MD (GT)
\(\widehat{AMB}=\widehat{DMB}\)=900
BM: cạnh chung
=> tam giác ABM = tam giác DBM (c.g.c)
=> \(\widehat{ABM}=\widehat{DBM}\) (2 góc tương ứng)
=> BM hay BC là phân giác góc ABD (đpcm)
Xét tam giác ACM và tam giác DCM có:
AM = MD (GT)
\(\widehat{AMC}=\widehat{DMC}\)=900
CM: cạnh chung
=> tam giác ACM = tam giác DCM (c.g.c)
=> \(\widehat{ACM}=\widehat{DCM}\) (2 góc tương ứng)
=> CM hay CB là phân giác góc ACD (đpcm)
10 tháng 7 2017
Vì OA là tia phân giác của xOC => xOA=AOC=12.xOCxOA=AOC=12.xOC (1)
Vì OB là tia phân giác của COy => COB=BOy=12.COyCOB=BOy=12.COy (2)
Từ (1) và (2) => xOA+BOy=AOC+BOC=12.xOC+12.COyxOA+BOy=AOC+BOC=12.xOC+12.COy
=> xOA+BOy=AOB=12.(xOC+COy)xOA+BOy=AOB=12.(xOC+COy)
=> 90o=12.xOy90o=12.xOy
=> xOy=90:12xOy=90:12
=> xOy = 90.2 = 180 => là góc bẹt
=> Ox và Oy là 2 tia đối nhau
Vậy Ox và Oy là 2 tia đối nhau
hihi
M
9 tháng 10 2019
TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt
16 tháng 3 2017
A O B t y z
Ot là phân giác của \(\widehat{AOB}\)=>\(\widehat{AOT}=\widehat{BOT}\)(1). \(Oy\)là phân giác của \(\widehat{BOT}\Rightarrow\widehat{tOy}=\widehat{BOy}=\frac{1}{2}\widehat{BOt}\)(2)
\(Oz\)là phân giác của \(\widehat{AOt}\Rightarrow\widehat{AOz}=\widehat{tOz}=\frac{1}{2}\widehat{AOt}\)(3)
Từ (1);(2);(3)=> \(\widehat{tOz}=\widehat{tOy}\)và Ot nằm giữa Oz và Oy => Ot là phân giác của \(\widehat{yOz}\).
Bài 6: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{142^0}{2}=71^0\)
Ta có: \(\widehat{xOz}+\widehat{x'Oz}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oz}+71^0=180^0\)
=>\(\widehat{x'Oz}=109^0\)
Bài 7:
Ta có: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}=90^0\)
Ot là phân giác của góc xOz
=>\(\widehat{zOt}=\dfrac{\widehat{xOz}}{2}=\dfrac{90^0}{2}=45^0\)
Ov là phân giác của góc yOz
=>\(\widehat{vOz}=\dfrac{90^0}{2}=45^0\)
\(\widehat{vOt}=\widehat{zOv}+\widehat{zOt}=45^0+45^0=90^0\)