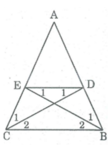
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm E sao cho AE=AB/3; trên cạnh AC lấy điểm D sao cho CD=AC/3.Tia ED cắt BC tại I.Chứng minh ED=EI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K

Vì AD=AE.
=>tg ADE cân tại A.
Vậy, suy ra: góc ADE= góc ABC(vì cả 2 tg đều cân tại A nên các góc ở đáy bằng nhau).
Mà góc ADE và góc ABC ở vi trí đồng vị.
=>DE // BC.

AD = AE (gt)
⇒ ∆ ADE cân tại A ⇒ ∠ (ADE) = ( 180 0 - ∠ A )/2
∆ ABC cân tại A ⇒ ∠ (ABC) = ( 180 0 - ∠ A )/2
Suy ra: ∠ (ADE) = ∠ (ABC)
⇒ DE // BC (Vì có cặp góc đồng vị bằng nhau)
Tứ giác BDEC là hình thang
∠ (ABC) = ∠ (ACB) (tính chất tam giác cân) hay ∠ (DBC) = ∠ (ECB)
Vậy BDEC là hình thang cân.

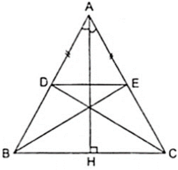
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.
có vẽ hình ko bạn
A B C I E D