Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc FEB+góc FBE=45+45=90 độ
=>EF vuông góc BC
b: ΔDFC vuông tại F có góc C=45 độ
nên ΔDFC vuông cân tại F
=>FD=FC
c: Xét ΔBEC có
EF,CA là đường cao
EF cắt CA tại D
=>D là trực tâm
=>BD vuông góc CE

gọi K là giao của ED và BC
ΔAED vuông tại A có AD=AE
nên ΔAED vuông cân tại A
góc KCE+góc KEC=45+45=90 độ
=>ED vuông góc BC

a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
Suy ra: DB=DE
b: Xét ΔDBH và ΔDEC có
góc DBH=góc DEC
DB=DE
góc BDH=góc EDC
Do đó: ΔDBH=ΔDEC
c: Ta có: ΔDBH=ΔDEC
nên góc DHB=góc DCE
d: Ta có: AH=AB+BH
AC=AE+EC
mà AB=AE; BH=EC
nên AH=AC

a: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
b: Xét ΔABE và ΔADE có
AB=AD
\(\widehat{BAE}=\widehat{DAE}\)
AE chung
Do đó: ΔABE=ΔADE
Suy ra: EB=ED
c: Xét ΔBEG và ΔDEC có
BE=DE
\(\widehat{BEG}=\widehat{DEC}\)
EG=EC
Do đó: ΔBEG=ΔDEC
Suy ra: \(\widehat{EBG}=\widehat{EDC}\)
=>\(\widehat{EBG}+\widehat{ADE}=180^0\)
=>\(\widehat{EBG}+\widehat{EBA}=180^0\)
=>A,B,G thẳng hàng

a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
=>ΔABC=ΔADE
b: góc DEB+góc CBA=45+45=90 độ
=>DE vuông góc BC tại H
c: Sửa đề: H là giao của DE với BC
Xét ΔHEB vuông tại H có góc HEB=45 độ
nên ΔHEB vuông cân tại H
=>HE=HB
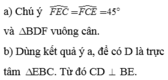
có vẽ hình ko bạn
A B C I E D