Cm không tồn tại 1 tam giác có độ dài 3 đường cao : 1; căn 3; căn 3 + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
Chứng minh rằng không tồn tại một tam giác có độ dài ba đường cao là 1; 3 ; 3 + 1 ( cùng đơn vị đo).
1
CM
21 tháng 2 2019
Giả sử tồn tại một tam giác có độ dài các đường cao là : h 1 = 1; h 2 = √3; h 3 = 1 + √3 (cùng đơn vị đo )
Gọi a 1 ; a 2 ; a 3 lần lượt là độ dài ba cạnh tương ứng với các đường cao h 1 ; h 2 ; h 3 .
Ta có: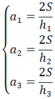 
a 1 ; a 2 ; a 3 lần lượt là 3 cạnh của tam giác nên:
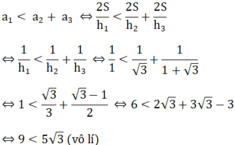
Vậy không tồn tại một tam giác có độ dài 3 đường cao lần lượt là 1; 3 1 + 3 (cùng đơn vị đo)
TT
0
22 tháng 10 2021
Bài 1:
\(CH=24\cdot\dfrac{3}{8}=9\left(cm\right)\)
\(DH=15\left(cm\right)\)
\(OC=\sqrt{9\cdot24}=6\sqrt{6}\left(cm\right)\)
\(OD=\sqrt{24^2-216}=6\sqrt{10}\left(cm\right)\)
\(OH=3\sqrt{15}\left(cm\right)\)
5 tháng 6 2017
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
9 tháng 7 2019
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
22 tháng 10 2021
Bài 1:
\(CH=24\cdot\dfrac{3}{8}=9\left(cm\right)\)
DH=15(cm)
\(OH=3\sqrt{15}\left(cm\right)\)
\(OC=\sqrt{OH^2+CH^2}=\sqrt{81+135}=6\sqrt{6}\left(cm\right)\)
\(OD=\sqrt{24^2-216}=6\sqrt{10}\left(cm\right)\)
.png)
4 tháng 3 2020
Gọi 3 cạnh của tam giác có độ dài là x, y, z
⇒⇒ x+y+z=60x+y+z=60
Như ta đã học, diện tích tam giác =12.h.a=12.h.a
Trong đó a là một cạnh của tam giác; h là chiều cao hạ từ một đỉnh lên cạnh a
Áp dụng vào bài này ta có: 12.12.x=12.15.y=12.20.z12.12.x=12.15.y=12.20.z
Vì bài này 3 cạnh có thể coi như nhau, nên có thể hoán đổi vị trí của chúng
Rút ra thay vào, ta được tam giác thỏa mãn yêu cầu bài toán có 3 cạnh là 36cm;2,4cm;21,6cm