Cho đường tròn (O) có M nằm ngoài (O), qua M vẽ tiếp tuyến MB với (O) (B là tiếp điểm ) . Kẻ BH vuông góc với OM tại H. Gọi I là giao điểm của đoạn thẳng OM và (O). Vẽ đường tròn (I , IH)
Chứng minh MB là tiếp tuyến của (I)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

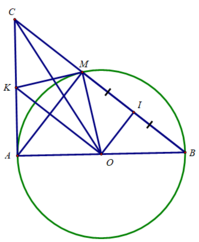
c) Tam giác CMA vuông tại M có MK là trung tuyến
⇒ MK = KA = KC
Xét Δ KAO và Δ KMO có:
KA = KM
KO là cạnh chung
AO = MO ( = bán kính (O))
⇒ Δ KAO = Δ KMO (c.c.c)
⇒ ∠(KAO) = ∠(KMO)
Mà ∠(KAO) = 90 0 ⇒ ∠(KMO) = 90 0
⇒ KM là tiếp tuyến của (O)

a: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>I là trung điểm của AB
Xét ΔMAK và ΔMCA có
góc MAK=góc MCA
góc AMK chung
=>ΔMAK đồng dạng với ΔMCA
=>MA/MC=MK/MA
=>MA^2=MC*MK=MI*MO
=>MC/MO=MI/MK
=>MC/MI=MO/MK
=>ΔMCO đồng dạng với ΔMIK

a: Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
Suy ra: MB là tiếp tuyến của (O)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét đường tròn (O) có tiếp tuyến MB tại B nên
\(\widehat{MBI}=\dfrac{1}{2}sđ\stackrel\frown{IB}\)
Lại có \(\widehat{IBH}=90^o-\widehat{BIH}\)
\(=90^o-\widehat{OIB}\)
\(=90^o-\dfrac{180^o-\widehat{IOB}}{2}\)
\(=\dfrac{180^o-180^o+sđ\stackrel\frown{IB}}{2}\)
\(=\dfrac{1}{2}sđ\stackrel\frown{IB}\)
Do đó \(\widehat{MBI}=\widehat{IBH}\) hay BI là tia phân giác của \(\widehat{MBH}\)
\(\Rightarrow d\left(I,MB\right)=d\left(I,BH\right)=IH=R_I\)
Suy ra MB là tiếp tuyến của (I)