K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 4 2022
Câu 3:
a: Xét ΔABC có AB<BC
nên \(\widehat{ACB}< \widehat{BAC}\)
b: Xét ΔABM có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABM cân tại A
mà \(\widehat{B}=60^0\)
nên ΔABM đều
S
2
15 tháng 10 2018
một sân trường hình chữ nhật có nửa chu vi là 120 .Chiều rộng bằng 3%5 chiều dài. Hỏi diện tích của sân trường đó bằng bao nhiêu mét vuông, bao nhiêu héc-ta
QC
12 tháng 3 2020
Đánh số cho các điểm từ trái qua phải, từ trên xuống dưới theo thứ tự 1 đến 9. Lấy điểm A nằm trên và cách 1 một khoảng đúng bằng khoảng cách giữa các điểm cho trước. Tương tự, lấy B là điểm nằm bên phải 9.
Lần lượt nối các điểm đã đánh dấu với nhau theo thứ tự dưới đây, lưu ý không nhấc bút khi chưa hoàn thành.
Đường 1 : 7 - 4 - 1 - A
Đường 2 : A - 2 - 6 - B
Đường 3 : B - 9 - 8 - 7
Đường 4 : 7- 5 - 3
4 tháng 1 2022
Câu 19:
19.1
Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{COD}=\widehat{COM}+\widehat{DOM}=\dfrac{1}{2}\cdot180^0=90^0\)
19.2 CM+MD=DC
mà CM=CA
và MD=DB
nên DC=CA+BD
19.3
Xét ΔCOD vuông tại O có OM là đường cao
nên \(OM^2=MC\cdot MD\)
\(\Leftrightarrow R^2=AC\cdot BD\)
Vậy: Tích ACxBD không đổi
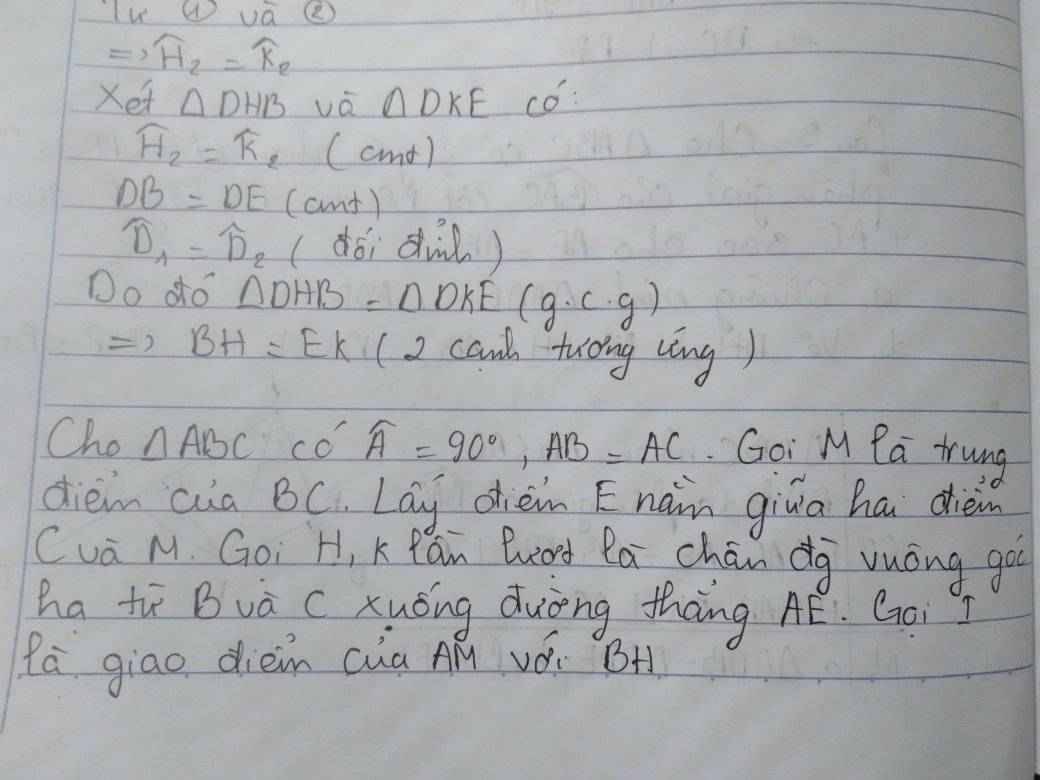
là sao hả bạn
giai cái j mới dc chứ