
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

22 tháng 7 2021
1.
a. Ta có: \(AB^2+AC^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\) \(\Rightarrow\Delta\)ABC vuông tại A
b. \(\Delta\)ABC vuông tại A, đường cao AH. Ta có:
AB.AC = AH.BC
hay 6.8 = AH.10
=> AH = \(\dfrac{6.8}{10}=4.8\)

16 tháng 1 2023
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: góc ABH+góc EBC=góc ABC
góc ACK+góc ECB=góc ACB
mà góc ABH=góc ACK;góc ABC=góc ACB
nên góc EBC=góc ECB
=>ΔEBC cân tại E
c: AB=AC
EB=EC
=>AE là trung trực của BC
=>AE vuông góc với BC
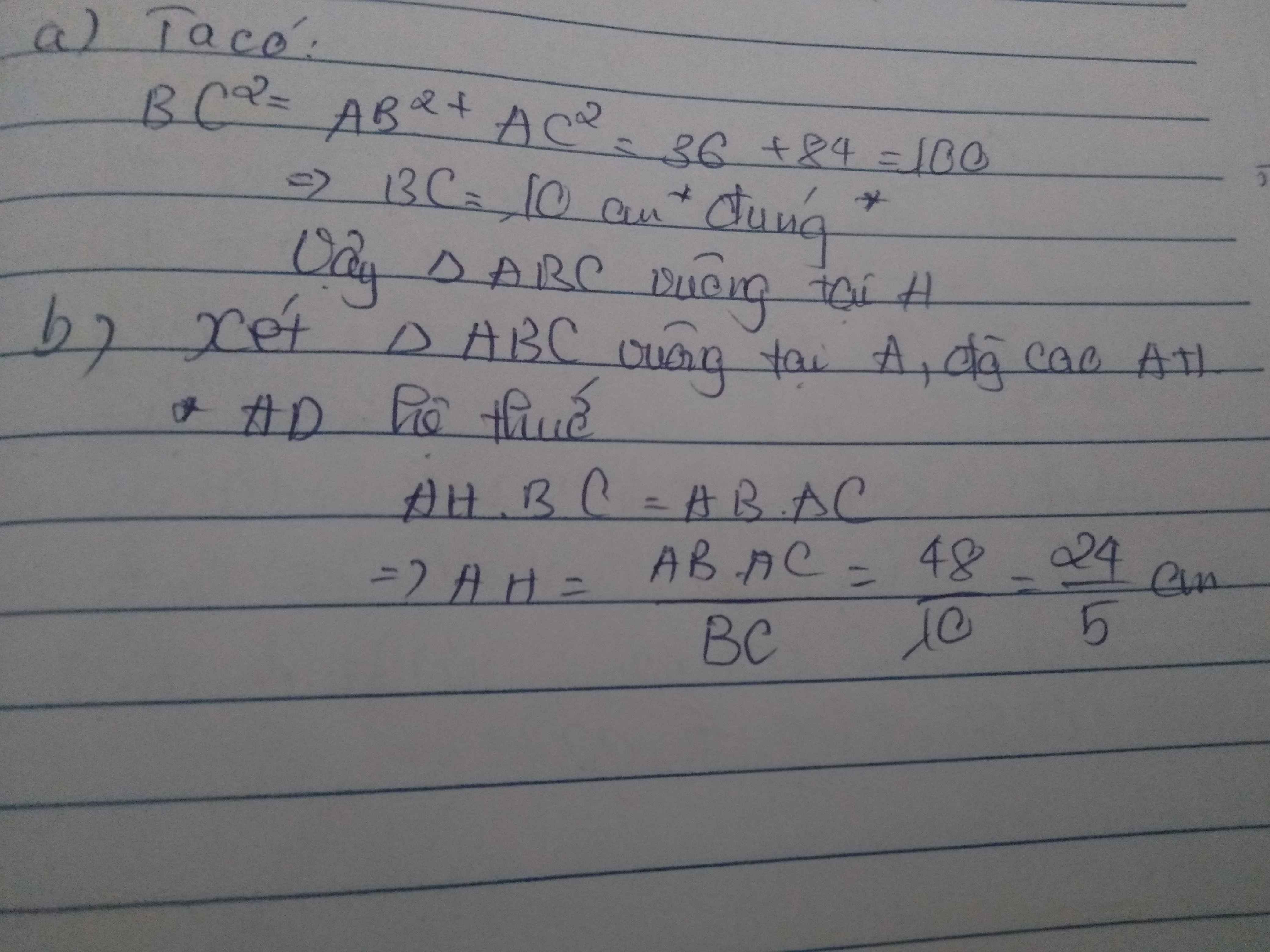


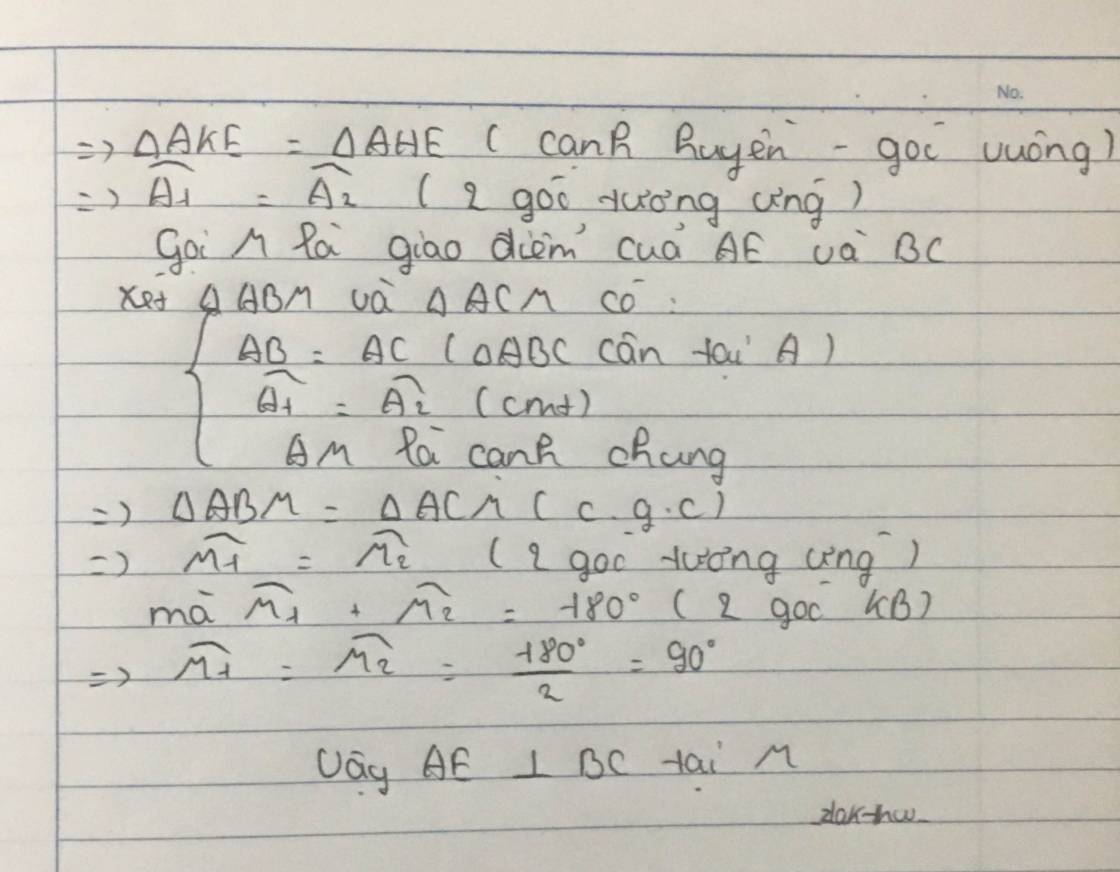
Bài 5:
Áp dụng BĐT Cô si cho 2 số: \(\sqrt{\dfrac{b+c}{a}}\) và 1
Có:
\(\sqrt{\dfrac{b+c}{a}}.1\le\dfrac{\left(\dfrac{b+c}{a}+1\right)}{2}\)
\(\Rightarrow\sqrt{\dfrac{b+c}{a}}\le\dfrac{a+b+c}{2a}\)
\(\Rightarrow\sqrt{\dfrac{a}{b+c}}\ge\dfrac{2a}{a+b+c}\)
Tương tự: \(\sqrt{\dfrac{b}{a+c}}\ge\dfrac{2b}{a+b+c}\)
\(\sqrt{\dfrac{c}{a+b}}\ge\dfrac{2c}{a+b+c}\)
\(\Rightarrow\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{a+c}}+\sqrt{\dfrac{c}{a+b}}\ge\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}\Rightarrow VT\ge2\Rightarrow VT>1\)