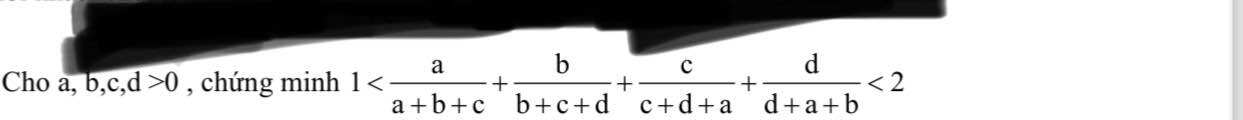 cần gấp ạ 🫰🏻
cần gấp ạ 🫰🏻
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(a-b\right)-\left(2c-4a\right)+3c\)
\(=a-b-2c+4a+3c\)
\(=5a-b+c\)
b) \(\left(12-60\right)-\left(2.-135-4.12\right)+3.-135\)
\(=-48-\left(-318\right)+\left(-405\right)\)
\(=-135\)
Bài 1:
a, A=(a-b)-(2c-4a)+3c
=a-b-2c+4a+3c
=5a-b+c
b, thay a=12; b=60; c=-135
A=5*12-60+(-135)
A=-135
Bài 2:
a, (a-b)+(c-d)-(a+c)
=a-b+c-d-a-c
=-b-d
=-(b+d) (đpcm)
b, (a-b)-(c-d)+(b+c)
=a-b-c+d+b+c
=a+d (xem lại đề bài bạn)
Chúc may mắn

(a + b)(c + d) - (a + d)(b + c)
= a(c + d) + b(c + d) - [ a(b + c) + d(b + c)]
= ac + ad + bc + bd - [ ab + ac + bd + cd]
= ac + ad + bc + bd - ab - ac - bd - cd
= (ac - ac) + (bd - bd) + ad + bc - ab - cd
= ad + bc - ab - cd
= ad - ab - cd + bc
= a(d - b) - c(d - b)
= (a - c)(d - b) (ĐPCM)

Câu hỏi của Adminbird - Toán lớp 7 - Học toán với OnlineMath
Câu hỏi của Adminbird - Toán lớp 7 - Học toán với OnlineMath

Ta có:
Vế trái: -a.(c-d)-d.(a+c)
=-ac+ad-ad-cd
=-ac-cd (1)
Vế phải: -c(a+d)=-ac-cd (1)
Vì (1)=(2)
<=> -a.(c-d)-d.(a+c)=-c.(a+d) (đpcm)
(Lưu ý: "đpcm" nghĩa là "điều phải chứng minh".)
Lời giải:
1) \(VT=-a.\left(c-d\right)-d.\left(a+c\right)\)
$=-ac+ad-da-dc$
$=-ac-dc$
$=-c(a+d) (đpcm)$
$2) (3a+2).(2a-1)+(3-a).(6a+2)-17.(a-1)$
$=6a^2-3a+4a-2+18a+6-6a^2-2a-17a+17$
$=21$
Vậy giá trị biểu thức không phụ thuộc vào a

1.a) Để B là phân số \(\Leftrightarrow n+5\ne0\Rightarrow n\ne5\)
b) Để b là số nguyên \(n-3⋮n+5\)
mà \(n+5⋮n+5\Rightarrow n-3-\left(n+5\right)⋮n+5\Rightarrow-8⋮n+5\) \(n+5\inƯ\left(-8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
Ta có bảng sau:
| n+5 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| n | -4 | -6 | -3 | -7 | -1 | -9 | 3 | -13 |
Vậy n=-4;-6;-3;-7;-1;-9;3;-13
2.
Vì\(\frac{a}{b}=\frac{c}{d}\Rightarrow\hept{\begin{cases}a=ct\\b=dt\end{cases}\left(t\in Z,t\ne0\right)}\)
a)\(\frac{a+c}{b+d}=\frac{ct+c}{dt+d}=\frac{c\left(t+1\right)}{d\left(t+1\right)}=\frac{c}{d}=\frac{a}{b}\)
b)\(\frac{a-c}{b-d}=\frac{ct-c}{dt-d}=\frac{c\left(t-1\right)}{d\left(t-1\right)}=\frac{c}{d}=\frac{a}{b}\)
Cái câu 2: Hoàng Nguyễn Văn làm có j đó sai sai
Đây:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)(1)
Suy ra: \(\orbr{\begin{cases}a=bk\\c=dk\end{cases}}\)
Suy ra: \(a+c=bk+dk=k\left(b+d\right)\)
Suy ra \(\frac{a+c}{b+d}=k\)(2)
Từ (1) và (2) => đpcm

Ta có: \(\frac{a}{b}=\frac{a+c}{b+d}\)
\(\Leftrightarrow a\left(b+d\right)=b\left(a+c\right)\\ \Leftrightarrow ab+ad=ab+bc\\ \Leftrightarrow ad=bc\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)
=> ĐPCM.
ta có: \(\frac{a}{b}=\frac{a+c}{b+d}\) \(\Rightarrow a\left(b+d\right)=b\left(a+c\right)\)
\(\Leftrightarrow ab+ad=ba+bc\)
\(\Leftrightarrow ad=bc\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)
Vậy \(\frac{a}{b}=\frac{a+c}{b+d}\) \(\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....

a) Giải:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk,c=dk\)
Ta có:
\(\frac{ab}{cd}=\frac{bkb}{dkd}=\frac{b^2}{d^2}\) (1)
\(\frac{a^2-b^2}{c^2-d^2}=\frac{\left(bk\right)^2-b^2}{\left(dk\right)^2-d^2}=\frac{b^2.k^2-b^2}{d^2.k^2-d^2}=\frac{b^2.\left(k^2-1\right)}{d^2.\left(k^2-1\right)}=\frac{b^2}{d^2}\) (2)
Từ (1) và (2) suy ra \(\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\left(đpcm\right)\)
b) Giải:
Để \(P\in Z\Rightarrow2x-3⋮x+1\)
Ta có:
\(2x-3⋮x+1\)
\(\Rightarrow\left(2x+2\right)-5⋮x+1\)
\(\Rightarrow5⋮x+1\)
\(\Rightarrow x+1\in\left\{1;-1;5;-5\right\}\)
+) \(x+1=1\Rightarrow x=0\)
+) \(x+1=-1\Rightarrow x=-2\)
+) \(x+1=5\Rightarrow x=4\)
+) \(x+1=-5\Rightarrow x=-6\)
Vậy \(x\in\left\{0;-2;4;-6\right\}\)
\(\Rightarrow5⋮x+1\)
1)Ta có:\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
\(\Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\frac{a}{c}\cdot\frac{b}{d}=\frac{ab}{cd}=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2-b^2}{c^2-d^2}\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\left(đpcm\right)\)
2)\(P=\frac{2x-3}{x+1}=\frac{2x+2-5}{x+1}=\frac{2\left(x+1\right)-5}{x+1}=2-\frac{5}{x+1}\)
\(\Rightarrow P\in Z\Leftrightarrow2-\frac{5}{x+1}\in Z\Leftrightarrow\frac{5}{x+1}\in Z\Leftrightarrow5⋮x+1\Leftrightarrow x+1\inƯ\left(5\right)\)
\(\Rightarrow x+1\in\left\{-1;-5;1;5\right\}\)
\(\Rightarrow x\in\left\{-2;-6;0;4\right\}\)
Lời giải:
Ta thấy, với $a,b,c,d>0$ thì:
$\frac{a}{a+b+c}+\frac{b}{b+c+d}+\frac{c}{c+d+a}+\frac{d}{d+a+b}> \frac{a}{a+b+c+d}+\frac{b}{a+b+c+d}+\frac{c}{a+b+c+d}+\frac{d}{a+b+c+d}=\frac{a+b+c+d}{a+b+c+d}=1(*)$
Lại có:
Xét $\frac{a}{a+b+c}-\frac{a+d}{a+b+c+d}=\frac{-d(b+c)}{(a+b+c)(a+b+c+d)}<0$ với mọi $a,b,c,d>0$
$\Rightarrow \frac{a}{a+b+c}< \frac{a+d}{a+b+c+d}$
Tương tự: $\frac{b}{b+c+d}< \frac{b+a}{a+b+c+d}, \frac{c}{c+d+a}< \frac{c+b}{a+b+c+d}; \frac{d}{d+a+b}< \frac{d+c}{a+b+c+d}$
Cộng lại suy ra:
$\frac{a}{a+b+c}+\frac{b}{b+c+d}+\frac{c}{c+d+a}+\frac{d}{d+a+b}< \frac{a+d+b+a+c+b+d+c}{a+b+c+d}=\frac{2(a+b+c+d)}{a+b+c+d}=2(**)$
Từ $(*); (**)\Rightarrow$ đpcm.