mn lm giup e vs a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
1
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
1 tháng 3 2022
a: \(\Leftrightarrow2x^2+6x-3x-9=0\)
=>(x+3)(2x-3)=0
=>x=3/2 hoặc x=-3
b: \(\Leftrightarrow6x\left(1-2x\right)=0\)
=>x=0 hoặc 1-2x=0
=>x=0 hoặc x=1/2
c: \(\Leftrightarrow8x^2=1\)
\(\Leftrightarrow x^2=\dfrac{2}{16}\)
hay \(x\in\left\{\dfrac{\sqrt{2}}{4};-\dfrac{\sqrt{2}}{4}\right\}\)
d: \(\Leftrightarrow x^4-9x^2+2x^2-18=0\)
\(\Leftrightarrow x^2-9=0\)
=>x=3 hoặc x=-3
5 tháng 8 2021
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(60^0< 120^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
Suy ra: \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
hay \(\widehat{yOz}=60^0\)
b) Ta có: tia Oy nằm giữa hai tia Ox và Oz(cmt)
mà \(\widehat{xOy}=\widehat{yOz}\left(=60^0\right)\)
nên Oy là tia phân giác của \(\widehat{xOz}\)
2 tháng 7 2023
a: \(P=\dfrac{a+1+\sqrt{a}}{a+1}:\dfrac{a+1-2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(a+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1}{a+1}\cdot\dfrac{\left(a+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)^2}=\dfrac{a+\sqrt{a}+1}{\sqrt{a}-1}\)
b: P<1
=>P-1<0
=>\(\dfrac{a+\sqrt{a}+1-\sqrt{a}+1}{\sqrt{a}-1}< 0\)
=>căn a-1<0
=>0<a<1
c: Thay x=19-8căn3 vào P, ta được:
\(P=\dfrac{19-8\sqrt{3}+4+\sqrt{3}+1}{4+\sqrt{3}-1}=\dfrac{31-15\sqrt{3}}{2}\)
NL
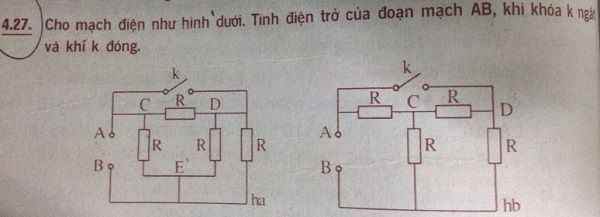cho e hỏi bai này vs ạ mong mn lm giúp e e đang cần rất gấp
0
mn giup mk lm bai nay voi a
25 tháng 4 2021
bn nhớ tick cho mình nha
7a
bn ko chụp câu 8
9a
10c
11b
12d
13a
b1: \(\dfrac{1}{-3}=\dfrac{-1}{3}=\dfrac{-10}{30}\)
\(\dfrac{-1}{4}=\dfrac{-10}{40}\)
=>3 số hữu tỉ xen giữa là \(-\dfrac{10}{31};-\dfrac{10}{33};-\dfrac{10}{37}\)
b2: \(\dfrac{-3}{7}=\dfrac{-3\cdot5}{7\cdot5}=\dfrac{-15}{35}=\dfrac{-150}{350};\dfrac{-2}{5}=\dfrac{-2\cdot7}{5\cdot7}=\dfrac{-14}{35}=-\dfrac{140}{350}\)
=>3 số hữu tỉ xen giữa là \(-\dfrac{149}{350};-\dfrac{147}{350};-\dfrac{145}{350}\)