 Mình cảm ơn!! Cần giải gấp
Mình cảm ơn!! Cần giải gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi số đó là ab
ta có: ab=8x(a+b)
a x 10 + b =8 x a + 8 x b
a x 2=b x 7
vậy : ab =72
Gọi số đó là ab
Theo đề bài ta có:
ab = 8( a+ b )
10a + b = 8a + 8b
2a = 7b ( bớt mỗi bên đi 8a + b )
=> a = 7
b = 2
Vậy số cần tìm là 72


b: Gọi giao của AH với BC là F
=>AH vuông góc BC tại F
góic CHI=góc AHD=90 độ-góc HAD=góc ABC=1/2*sđ cung AC
góc CIH=1/2*sđ cung CA
=>góc CHI=góc CIH
=>ΔCHI cân tại C
c:
góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>MD=ME
=>ΔMDE cân tại M
mà MN là trung tuyến
nên MN vuông góc DE
Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AED
=>Ax//DE
=>DE vuông góc OA
=>MN//AO

Bài 2:
b: 2x-4y=5
=>4y=2x+5
=>y=1/2x+5/4
Vậy: Hệ số góc là 1/2

Ta có: \(AB^2+HC^2=\left(AA'^2+A'B^2\right)+\left(A'H^2+A'C^2\right)\)
\(=\left(AA'^2+A'C^2\right)+\left(A'B^2+A'H^2\right)=AC^2+HB^2\)
Lại có: \(BC^2+HA^2=\left(BB'^2+B'C^2\right)+\left(B'H^2+B'A^2\right)\)
\(=\left(BB'^2+B'A^2\right)+\left(B'C^2+B'H^2\right)=AB^2+HC^2\)
\(\Rightarrow AB^2+HC^2=AC^2+HB^2=BC^2+HA^2\)

22.
ĐKXĐ: \(y\ne1\)
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{y-1}=2\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+\dfrac{2}{1-y}=4\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
Trừ pt dưới cho trên:
\(\Rightarrow\dfrac{1}{1-y}=-2\)
\(\Rightarrow1-y=-\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\)
Thế vào \(x^2-\dfrac{1}{y-1}=2\)
\(\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right);\left(-2;\dfrac{3}{2}\right)\)
b.
ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
\(Hệ\Leftrightarrow\left\{{}\begin{matrix}2y^2-\dfrac{10}{2x+1}=8\\2y^2-\dfrac{11}{2x+1}=7\end{matrix}\right.\)
Trừ pt trên cho dưới:
\(\Rightarrow\dfrac{1}{2x+1}=1\)
\(\Rightarrow2x+1=1\)
\(\Rightarrow x=0\)
Thế vào \(y^2-\dfrac{5}{2x+1}=4\)
\(\Rightarrow y^2=9\Rightarrow y=\pm3\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;3\right);\left(0;-3\right)\)





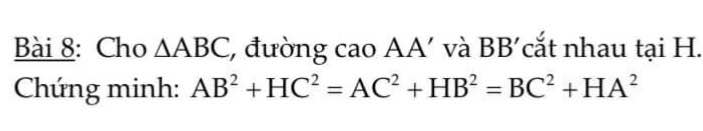




a/
$A=x^2-4x+10=(x^2-4x+4)+6=(x-2)^2+6$
Ta thấy:
$(x-2)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A=(x-2)^2+6\geq 6>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A$ luôn có giá trị dương với mọi giá trị $x$.
a/
$B=2x^2-2x+3=x^2+(x^2-2x+1)+2=x^2+(x-1)^2+2$
Ta thấy:
$x^2\geq 0; (x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B=x^2+(x-1)^2+2\geq 2>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B$ luôn có giá trị dương với mọi giá trị $x$.