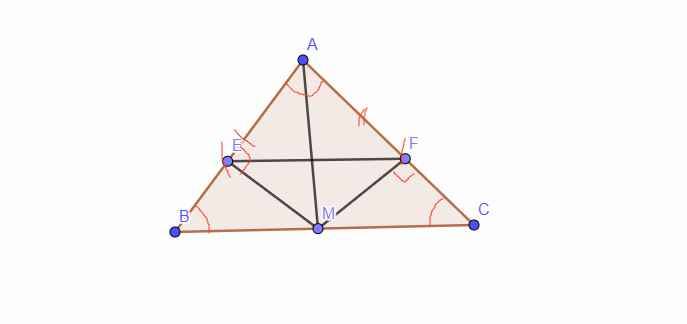
cho tam giác abc cân tại a, m là trung điểm bc kẻ me ⊥ ab , mf ⊥ ac a) chứng minh tam giác abm=acm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

Xét \(\Delta BCA:\)M là trung điểm BC ; \(ME\text{//}BC\left(E\in AB\right)\)
\(\Rightarrow ME\)là đường trung bình \(\Delta BCA\)
\(\Rightarrow E\) là trung điểm AB
Chứng minh tương tự được \(F\)là trung điểm AC
\(\Rightarrow EF\)là đường trung bình \(\Delta ABC\)
\(\Rightarrow EF\text{//}BC\)
Do đó BCFE là hình thang có \(\widehat{B}=\widehat{C}\)( \(\Delta ABC\)cân tại A) là 2 góc kề đáy BC bằng nhau nên là hình thang cân.
Vậy ...

a) xét ΔABM và ΔACM có
góc B = góc C
AB = AC ( ΔABC cân tại A )
BM=CM ( tính chất các đường của Δ cân từ đỉnh )
=> ΔABM = ΔACM
b) xét ΔBME và ΔCMF có
góc B bằng góc C
BM=CM
=> ΔBME=ΔCMF ( cạnh huyền góc nhọn )
=> FM = EM
=> ΔEMF cân tại M
c) gọi giao của EF và AM là O
ta có BE = CF => AE=AF
=> ΔAEF cân tại A
ta có AM là tia phân giác của góc A
mà O nằm trên AM suy ra AO cũng là tia phân giác của góc A
ta lại có ΔAEF cân tại A
suy ra AO vuông góc với EF
suy ra AM vuông góc với EF
xét ΔAEF và ΔABC có
EF và BC đều cùng vuông góc với AM => EF // BC
a) Xét ΔABM và ΔACM có
AB=AC(ΔABC cân tại A)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
BM=CM(M là trung điểm của BC)
\(\widehat{EBM}=\widehat{FCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(Cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng)
Xét ΔEMF có ME=MF(cmt)
nên ΔEMF cân tại M(Định nghĩa tam giác cân)

- Xét tam giác ABC vuông cân tại A có:
AO là trung tuyến ứng với cạnh huyền BC (O là trung điểm BC)
=>AO=BO=CO=\(\dfrac{1}{2}\)BC ; AO⊥BC tại O.
- Ta có: \(\widehat{EAF}=\widehat{AEM}=\widehat{AFM}=90^0\) nên AEMF là hình chữ nhật.
=> AE=MF ; AB//MF
- Ta có: \(\widehat{ABC}=\widehat{FMC}=45^0\) (AB//MF, tam giác ABC vuông cân tại A).
Mà tam giác MFC vuông tại F (MF⊥AC tại F) nên tam giác MFC vuông cân tại F.
=>MF=CF=AE.
- Ta có: Tam giác AOB vuông tại O (AO⊥BC tại O) mà AO=BO (cmt) nên tam giác AOB vuông cân tại O.
- Xét tam giác OAE và tam giác OCF có:
OA=OC (cmt)
\(\widehat{OCF}=\widehat{OAE}=45^0\) (tam giác ABC vuông cân tại A, tam giác AOB vuông cân tại O).
AE=CF (cmt)
=>Tam giác OAE= Tam giác OCF (c-g-c)
=> OE=OF (2 cạnh tương ứng).
\(\widehat{AOE}=\widehat{COF}\) (2 góc tương ứng) mà \(\widehat{COF}+\widehat{AOF}=90^0\) (AO⊥BC tại O).
nên \(\widehat{AOE}+\widehat{AOF}=90^0\) =>\(\widehat{EOF}=90^0\) =>Tam giác OEF vuông tại O mà OE=OF (cmt) nên tam giác OEF vuông cân tại O.

a: Xét ΔABC có
M là trung điểm của BC
ME//AC
=>E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
=>F là trung điểm của AC
Xét ΔABC có E,F lần lượt là trung điểm của AB,AC
=>EF là đường trung bình
=>EF//BC và EF=BC/2
b: ΔKAC vuông tại K có KF là trung tuyến
nên KF=AC/2
Xét ΔABC có ME//AC
nên ME/AC=BE/BA=1/2
=>ME=1/2AC
=>ME=KF
Xét tứ giác MKEF có
MK//EF
ME=KF
=>MKEF là hình thang cân

a: Xét tứ giác BMEC có ME//BC
nên BMEC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMEC là hình thang cân
b: Xét ΔABC có
M là trung điểm của AB
ME//BC
Do đó: E là trung điểm của AC
Xét ΔABC có
M là trung điểm của AB
MF//AC
Do đó: F là trung điểm của BC
Xét ΔABC có
M là trung điểm của AB
F là trung điểm của BC
Do đó: MF là đường trung bình của ΔBAC
Suy ra: \(MF=\dfrac{AC}{2}\)
mà \(EC=\dfrac{AC}{2}\)
nên MF=EC
Xét tứ giác MECF có
MF//EC
MF=EC
Do đó: MECF là hình bình hành
c: Xét ΔABC có
M là trung điểm của AB
E là trung điểm của AC
Do đó: ME là đường trung bình của ΔABC
Suy ra: ME//BC và \(ME=\dfrac{BC}{2}\)
mà \(BF=\dfrac{BC}{2}\)
nên ME//BF và ME=BF
Xét tứ giác MEFB có
ME//BF
ME=BF
Do đó: MEFB là hình bình hành
Suy ra: Hai đường chéo MF và BE cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của MF
nên I là trung điểm của BE
hay B,I,E thẳng hàng

Bài làm :
a) Xét tam giác BEM và tam giác CFM
Ta có: BM = MC ( vì M là trung điểm của BC)
M là góc chung
Do đó : tam giác BEM=CFM( cạnh huyền- góc nhọn)
b) Bạn ghi chưa hết đề nên mik ko hiểu
sorry ![]()
![]()

a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM