Cho hình thang ABCD (AB // CD) có BC = 15cm. Điểm E thuộc cạnh AD sao AE/AD = 1/3 cho AE . Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 10 2018
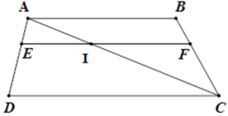
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
B F B C = A I A C = A E A D = 4 12 = 1 3 nên BF = 1 3 .BC = 1 3 .15 = 5 (cm)
Đáp án: B
CM
7 tháng 3 2018
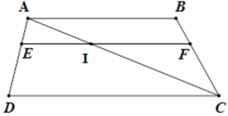
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
B F B C = A I A C = A E A D = 1 3 nên BF = 1 3 .BC = 1 3 .15 = 5 (cm)
Đáp án: B
CM
12 tháng 3 2017
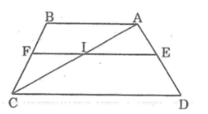
Kẻ đường chéo AC cắt EF tại I
Trong ΔADC, ta có: EI // CD
Suy ra: 
Suy ra: 
Lại có :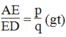 
Suy ra: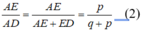 
Từ (1) và (2) suy ra: 
Trong ΔABC, ta có: FI // AB
Suy ra: 
(định lí ta-lét) (3)
Trong ΔADC, ta có : EI // CD
Suy ra: 
(định lí ta-lét) (4)
Từ (3) và (4) suy ra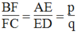 
Trong ΔABC, ta có: IF // AB
Suy ra: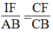 
(định lí ta-lét)
Suy ra: 
Ta có: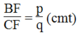 
Suy ra: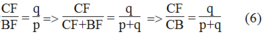 
Từ (5) và (6) suy ra: 
Vậy: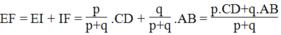 
4 tháng 2 2018
Kẻ đường chéo AC cắt EF tại G
EF // CD // AB hay EF // EG và GF // AB
Do EF // EG ,theo định lý Ta - let trong ΔADC :
AE/ED=AG/GC⇔AG/GC=42=2AE/ED=AG/GC⇔AG/GC=4/2=2
Do GF // AB ,theo định lý Ta - let trong ΔABC :
AG/GC=BF/FC⇔2=6/FC
⇒FC=3
18 tháng 3 2018
gọi giao điểm của AC và EF là O
có EO//CD(EF//CD;O\(\in\)EF)
=>\(\frac{AE}{AD}=\frac{EO}{CD}\)(hệ quả ta-lét)
=>\(\frac{1}{3}=\frac{EO}{4}\left(CD=4cm;\frac{AE}{AD}=\frac{1}{3}\right)\)
=> EO=\(\frac{4}{3}\)cm
có BF=\(\frac{1}{3}\)BC(gt)=>CF=(1-\(\frac{1}{3}\))BC=\(\frac{2}{3}\)BC
Có FO//AB(EF//CD;O\(\in\)EF)
=>\(\frac{CF}{CB}=\frac{FO}{AB}\)(hệ quả talet)
=>\(\frac{2}{3}=\frac{FO}{1}\left(\frac{CF}{CB}=\frac{2}{3};AB=1cm\right)\)
=>FO=\(\frac{2}{3}\)cm
Có EO+FO=EF(O\(\in\)EF)
=>EF=\(\frac{4}{3}\)+\(\frac{2}{3}\)=\(\frac{6}{3}\)=2cm
vậy độ dài EF=2cm
21 tháng 1 2022
Xét hình thang ABCD có EF//AB//CD
nên AE/ED=BF/FC
=>6/FC=2
hay FC=3(cm)
Áp dụng định lý Thales cho hình thang:
\(\dfrac{AE}{AD}=\dfrac{BF}{BC}\Rightarrow\dfrac{BF}{BC}=\dfrac{1}{3}\)
\(\Rightarrow BF=\dfrac{BC}{3}=\dfrac{15}{3}=5\left(cm\right)\)