Có 12 cặp vợ chồng tham gia một buổi liên hoan. Ban tổ chức chọn ngẫu nhiên 4 nam và 4 nữ tham gia 1 trò chơi. Tính xác suất để chọn được ít nhất 1 cặp vợ chồng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 12 2017
Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là C 12 3 = 220
b. Gọi B là biến cố :” trong 3 người được chọn không có cặp vợ chồng nào” thì B ¯ là biến cố :” có đúng một cặp vợ chồng trong ba người được chọn”
( vì có 3 cách chọn cặp vợ chồng, và 10 cách chọn người thứ 3 trong số 10 người còn lại) nên
Chọn D
CM
16 tháng 6 2019
Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là C_123= 220
a. Gọi A là biến cố:” trong 3 người được chọn có đúng 1 nam”
n(A)= C61. C62= 90. Do đó P(A) =90/220=9/22
Chọn B
CM
29 tháng 4 2018
Chọn B
Gọi 2 cặp vợ chồng là C1-V1 và C2-V2 (C=chồng, V=vợ).
* Số cách chọn ra 7 đôi:
- Đầu tiên chọn ra 7 nam trong 10 nam: C 10 7 (cách).
- Xếp 7 người nam này thành 1 hàng ngang, người đầu tiên có 12 cách ghép với nữ, người thứ hai có 11 cách, cứ như thế suy ra số cách ghép đôi là 12.11.10.9.8.7.6 (cách).
- Theo quy tắc nhân có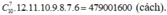 
* Số cách chọn 7 đôi, chỉ có một cặp vợ chồng
- Trường hợp 1: chỉ có cặp vợ chồng C1-V1, khi đó lấy 6 nam trong 9 nam còn lại:
+ Nếu trong 6 nam này không có C2 thì số cách ghép 6 cặp còn lại là: 
+ Nếu trong 6 nam này có C2 thì số cách ghép 6 cặp còn lại là: có 10 cách ghép C2 với nữ (trừ V2 và trừ V1), 5 nam còn lại có cách, số cách ghép cặp cho 5 nam này là 10.9.8.7.6 cách. Vậy theo quy tắc nhân có 
Theo quy tắc cộng, có 
- Trường hợp 2: chỉ có cặp vợ chồng C2-V2, tương tự như trên có 26248320(cách)
Vậy xác suất cần tính là: 
18 tháng 5 2023
\(n\left(\Omega\right)=C^3_{20}\)
A: "3 người được chọn ko có cặp vợ chồng nào"
=>\(\overline{A}\): 3 người được chọn có 1 cặp vợ chồng
=>\(n\left(\overline{A}\right)=C^1_4\cdot C^1_{18}=72\left(cách\right)\)
=>n(A)=1068
=>P=1068/1140=89/95
CH
5 tháng 1 2022
xin lỗi vì đã quá trễ nhưng giải cho người khác biết =(
thì tính kgm n(Ω)= 20C3
tiếp theo mk có biến cố A : " Ba người thì trong đó ko có 1 cặp vợ chồng nào"
\(\rightarrow\overline{A}:\)" Ba người trong đó có ít nhất 1 cặp vợ chồng" ( biến cố đối)
Chọn ra 1 cặp vợ chồng từ 4 cặp : 4C1 cách
- 1 cặp đã có sẵn 2 người r mà mình đã chọn 1 cặp thì số người còn lại là 18 người
=> 18C1 cách
\(P_{\overline{A}}=\dfrac{n\overline{A}}{n\Omega}\) \(=\dfrac{4C1.18C1}{20C3}\)
=> P(A) = 1 - P(\(\overline{A}\) ) => câu D nhóa
11 tháng 7 2018
câu 1) đặc các cặp vợ chồng lần lược là : \(A_1B_1;A_2B_2;A_3B_3....;A_{19}B_{19};A_{20}B_{20}\)
ta có : + số cách để chọn ra 4 người trong \(40\) người là : \(C^4_{40}\)
+ số cách để chọn ra 4 người mà không có cặp vợ chồng nào gồm
* cách chọn 4 người từ 20 người chồng là : \(C^4_{20}\)
* cách chọn 4 người từ 20 người vợ là : \(C^4_{20}\)
* số cách trộn lộn sộn đc tính như sau :
đặc 4 người đc chọn là : \(ABCD\)
\(\Rightarrow\) - \(A\) có 20 cách chọn
- \(B\) có 18 cách chọn
- \(C\) có 16 cách chọn
- \(D\) có 14 cách chọn
\(\Rightarrow\) có \(20.18.16.14=80640\) cách chọn
\(===\Rightarrow\) tổng cách chọn 4 người mà không có cặp vợ chồng nào là
\(C^4_{20}+C^4_{20}+80640\)
\(\Rightarrow\) sác xuất để chọn ra 4 người mà không có cặp vợ chồng nào là : \(P=\dfrac{C^4_{20}+C^4_{20}+80640}{C^4_{40}}=\dfrac{9033}{9139}\)
vậy .............................................................................................................................
câu còn lại để chiều về mk lm cho nha :)
11 tháng 7 2018
mk lm câu còn lại như lời hứa nha
câu 2 )
+ số cách chọn 5 người từ 22 người là : \(C^5_{22}\)
+ cách chọn ra 5 người nhưng không có cặp vợ chồng nào đc tác ra 5 trường hợp
ta đặc : các giáo viên nam lần lược là : \(A_1;A_2...;A_9\)
các giáo viên nữ lần lược là : \(B_1;B_2...;B_{13}\)
trong đó \(A_1;B_1vàA_2;B_2\) là 2 cặp vợ chồng
gọi các người được chọn là \(A;B;C;D;E\)
* th1: chọn 5 người đều là nam có : \(C^5_9\) cách
* th2: chọn 5 người đều là nữ có : \(C^5_{13}\)
* th3: \(A\in\left\{A_1;B_1;A_2;B_2\right\}\)
\(\Rightarrow\) \(A\) có 4 cách chọn ; và số cách chọn 4 người \(B;C;D;E\) từ 18 người còn lại là \(C^4_{18}\)
mà trường hợp này lại bao gồm số cách chọn 5 người cùng giới
\(\Rightarrow\) có \(10827\) cách chọn
* th4: \(A;B\in\left\{A_1;B_1;A_2;B_2\right\}\)
\(\Rightarrow\) \(A\) có 4 cách chọn ; \(B\) có 2 cách chọn ; và số cách chọn 3 người \(C;D;E\) từ 18 người còn lại là \(C^3_{18}\)
mà trường hợp này cũng bao gồm số cách chọn 5 người cùng giới
\(\Rightarrow\) có \(5115\) cách chọn
* th5: \(A;B;C;D;E\notin\left\{A_1;B_1;A_2;B_2\right\}\)
\(\Rightarrow\) số cách chọn \(5\) người \(A;B;C;D;E\) từ 18 người còn lại là \(C^5_{18}\)
mà trường hợp này cũng gồm trường hợp chọn phải 5 người cùng giới ; nhưng số cách chọn 5 người cùng giới ở trường hợp này đã giảm xuống còn \(C^5_7+C^5_{11}=483\) cách
\(\Rightarrow\) có \(8085\) cách chọn
\(===\Rightarrow\) sác xuất để chọn ra 5 người trong 22 người đó nhưng không có cặp vợ chồng nào là : \(P=\dfrac{C^5_9+C^5_{13}+10827+5115+8085}{C^5_{22}}=\dfrac{4240}{4389}\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
Chọn ngẫu nhiên 2 người từ 20 người ta được một tổ hợp chập 2 của 20. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\)( phần tử)
Gọi A là biến cố “Chọn được 2 người là vợ chồng”
Để chọn được 1 cặp vợ chồng lên khiêu vũ từ 10 cặp vợ chồng ta được một tổ hợp chập 1 của 10 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{10}^1\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^1}}{{C_{20}^2}} = \frac{1}{{19}}\)
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Cách chọn 2 bạn từ 7 bạn là \(C_{7}^2 \Rightarrow n\left( \Omega \right) = C_{7}^2 = 21\)
Gọi A là biến cố: “Hai bạn được chọn có một bạn nam và một bạn nữ”.
Cách chọn một bạn nam là: 3 cách chọn
Cách chọn một bạn nữ là: 4 cách chọn
Theo quy tắc nhân ta có \(n\left( A \right) = 3.4 = 12\)
Vậy xác suất của biến cố A là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{12}}{{21}} = \frac{4}{7}\).
Chọn A
DK
30 tháng 10 2017
Đáp án C
- Bên phía người vợ:
+ Cậu của người vợ có kiểu gen aa.
+ Ông bà ngoại của người vợ đều có kiểu gen Aa.
+ Mẹ của người vợ có kiểu gen 1/3AA:2/3Aa.
+ Bố của người vợ có kiểu gen 9/11AA:2/11Aa.
+ Người vợ có kiểu gen 5/8AA:3/8Aa.
- Bên phía người chồng:
+ Mẹ của người chồng kiểu gen aa.
+ Chị của người chồng kiểu gen aa.
+ Bố của người chồng có kiểu gen Aa.
+ Người chồng có kiểu gen Aa.
- Người con gái của người chồng 13/29AA:16/29Aa.
(1) đúng.
(2) đúng. 5/8AA:3/8Aa × Aa → 13/32AA:16/32Aa:3/32aa
→ XS cặp vợ chồng trên sinh đứa con thứ 2 không bị bệnh = 1/2A- = 29/64.
(3) sai: 13/29AA:16/29Aa × Aa → XS sinh một người con trai không bị bệnh = 1/2A- = 1/2(1-aa) = 1/2(1- 8/29 × 1/2) = 25/58.
(4) đúng