Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
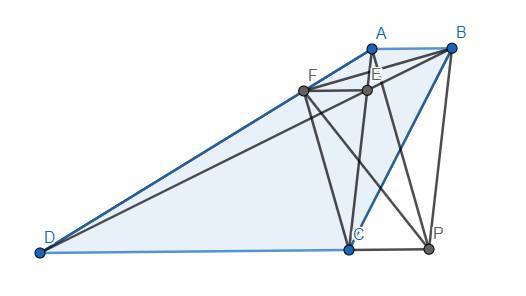
Dựng hình bình hành ABPC. Khi đó \(AD=AB+CD=CP+CD=DP\)
Ta có \(\dfrac{AB}{FE}=\dfrac{DA}{DF}\), \(\dfrac{CD}{FE}=\dfrac{DA}{AF}\)
\(\Rightarrow\dfrac{AB+CD}{FE}=DA\left(\dfrac{1}{DF}+\dfrac{1}{AF}\right)\)
\(\Rightarrow\dfrac{1}{FE}=\dfrac{DA}{DF.AF}\) \(\Rightarrow\dfrac{DF}{FE}=\dfrac{DP}{FA}\) \(\Rightarrow\dfrac{DF}{DC}=\dfrac{DP}{DA}=1\)
Từ đó \(\Delta DFC\) cân tại D. \(\Rightarrow\widehat{DFC}=\widehat{DCF}=\widehat{CFE}\) \(\Rightarrow\) FC là tia phân giác của \(\widehat{DFE}\). CMTT, FB là tia phân giác của \(\widehat{AFE}\). Do đó \(\widehat{BFC}=90^o\) (đpcm)
Có cặp tam giác có diện tích bằng nhau đó là:
- Diện tích tam giác ABD bằng diện tích tam giác ABC vì hai tam giác có chung đáy AB, chiều cao hạ từ D xuống đáy AB của tam giác ABD bằng chiều cao hạ từ C xuống đáy AB của tam giác ABC.
- Diện tích tam giác ADC bằng diện tích tam giác BDC vì hai tam giác có chung đáy DC, chiều cao hạ từ A xuống đáy DC của tam giác AD bằng chiều cao hạ từ B xuống đáy DC của tam giác BDC.
- Diện tích tam giác AOD bằng diện tích tam giác BOC
Vì nên hay
Vậy diện tích tam giác AOD bằng diện tích tam giác BOC
a: Vì AB//CD
nên \(\dfrac{AE}{CE}=\dfrac{BE}{DE}=\dfrac{AB}{CD}=\dfrac{1}{2}\)
Vì AE/CE=1/2 nên \(CE=2AE\)
=>\(S_{BCE}=2\times S_{ABE}\)(1)
Vì CE=2AE
nên \(S_{AED}=2\times S_{AEB}\left(2\right)\)
Từ (1),(2) suy ra \(S_{AED}=S_{BEC}\)
Kẻ AM,BN lần lượt vuông góc với DC
=>AM//BN
Xét tứ giác ABNM có
AB//NM
AM//BN
Do đó: ABNM là hình bình hành
=>AM=BN
\(S_{ADC}=\dfrac{1}{2}\times AM\times DC\)
\(S_{BDC}=\dfrac{1}{2}\times BN\times DC\)
mà AM=BN
nên \(S_{ADC}=S_{BDC}\)
Kẻ CF,DH lần lượt vuông góc với AB
=>CF//DH
Xét tứ giác CFHD có
CF//HD
HF//DC
Do đó: CFHD là hình chữ nhật
=>DH=CF
\(S_{DAB}=\dfrac{1}{2}\times DH\times AB\)
\(S_{CAB}=\dfrac{1}{2}\times CF\times AB\)
mà DH=CF
nên \(S_{DAB}=S_{CAB}\)
b: Xét ΔAKC có DE//KC
nên \(\dfrac{AD}{DK}=\dfrac{AE}{EC}=\dfrac{1}{2}\)