Viết thuật toán tính chu vi của hình tam giác ABC có độ dài 3 cạnh lần lượt là a, b, c dưới dạng sơ đồ khối
giúp mình với. Xin cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Cúc Hoa
Giáo viên
16 tháng 4
Đúng(0)
Những câu hỏi liên quan
17 tháng 12 2023
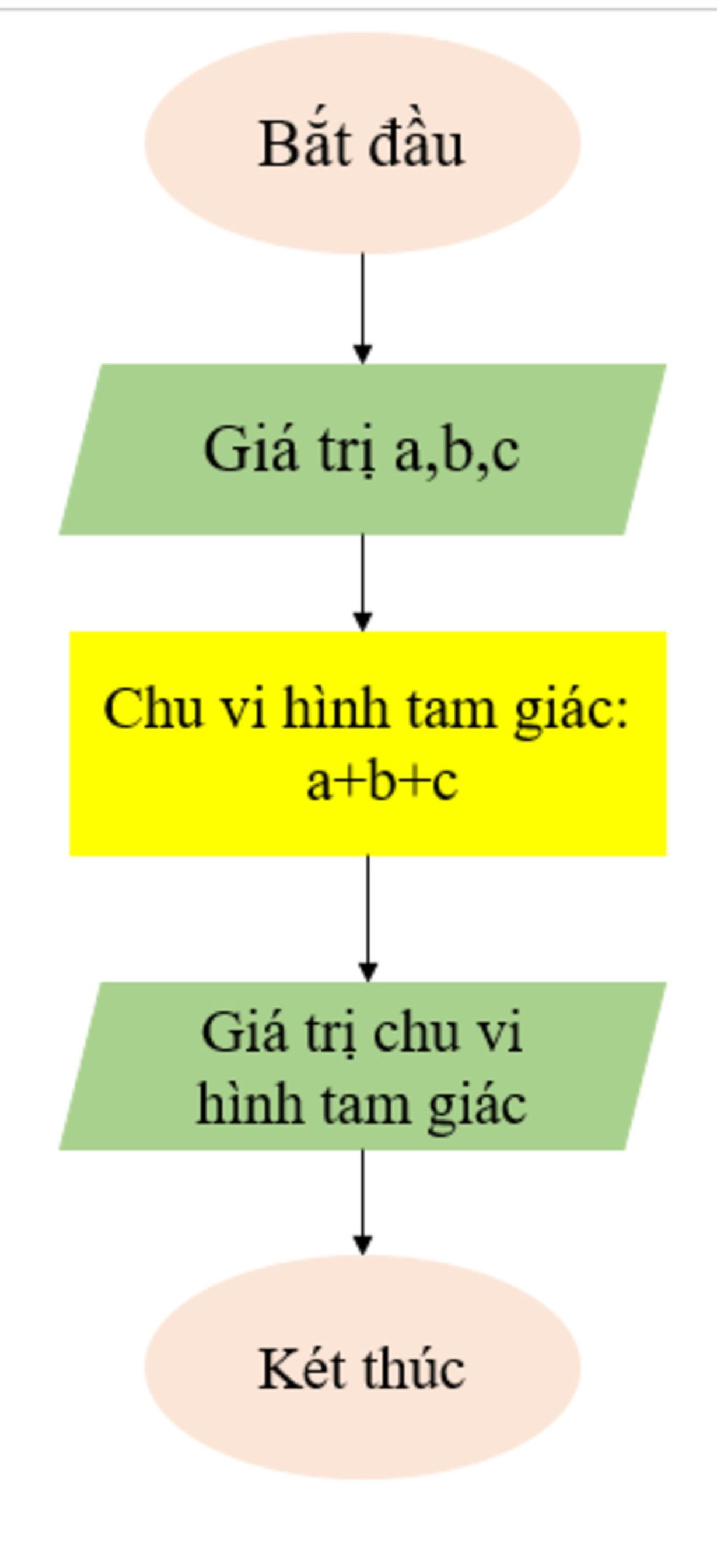
Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.
2 tháng 11 2021
uses crt;
var xa,ya,xb,yb,xc,yc,p,s,ab,bc,ac:real;
begin
clrscr;
readln(xa,ya,xb,yb,xc,yc);
ab:=sqrt(sqr(xa-xb)+sqr(ya-yb));
ac:=sqrt(sqr(xa-xc)+sqr(ya-yc));
bc:=sqrt(sqr(xb-xc)+sqr(yb-yc));
p:=(ab+bc+ac)/2;
s:=sqrt(p*(p-ab)*(p-ac)*(p-bc));
writeln(s:4:2);
readln;
end.
15 tháng 3 2016
Theo bất đẳng thức của tam giác ABC ta có : AB < AC+BC = AC < 1cm + 9cm => AB < 10cm (1)
Theo hệ quả bất đẳng thức tam giác ABC ta có: AB > BC-AC= AB > 9cm-1cm => AB > 8cm (2)
Từ (1) và (2) ta => 8cm< AB < 10cm => AB = 9cm
Chu vi tam giác ABC: AB+AC+BC = 9cm+9cm+1cm = 19cm
13 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
long long a,b,dt,cv;
int main()
{
cin>>a>>b;
cv=(a+b)*2;
dt=a*b;
cout<<"Chu vi la:"<<cv<<endl;
cout<<"Dien tich la:"<<dt;
return 0;
}
J
8 tháng 4 2020
a) vì M là tđ AB -> AM=1/2AB=5cm
N là tđ AC -> AN=1/2AC= 12cm
áp dụng pytago vào tam giác ANM => MN=13cm
b) theo công thức tính diện tích tam giác ANM (cái này mình chưa biết bạn học chưa, nếu chưa thì nhắn cho mình giải thích cho)
1/2(AM x AN) = 1/2(MN x AH)
=> AM x AN = MN x AH -> 5 x 12 = 13 x AH
=> AH=60/13cm
c) xét 2 tam giác BKM vuông tại K và AHM vuông tại H
có góc AMH + góc BMK ( đối đỉnh )
AM=MB ( M là Tđ AB)
=> 2 tam giác BKM=AHM (cạnh huyền góc nhọn)
d) áp dụng pytago vào tam giác AHM vuông tại H
AM2-AH2=HM2 => HM=MK=25/13cm (vì 2 tam giác ở câu c bằng nhau)
8 tháng 4 2020
tam giác ABC có góc A vuông
ta có : BC2 = AB2 +AC2 ( định lý pytago )
thay BC2 = 102 + 242
=> BC=26 cm
ta lại có : M là trung điểm của AB => AM=1/2AB=1/2 . 10 =5 cm
tương tự : N là trung điểm của AC => AN = 1/2AC = 1/2 .24 = 12 cm
tam giác AMN vuông tại A , ta có : MN2 = AM2 + AN2 ( định lí pytago )
thay MN2 = 52 + 122
=> MN = 13 cm
Vậy MN = 13 cm
30 tháng 12 2020
Bài 1:
Ý tưởng: Sau khi nhập bán kính r, chúng ta sẽ tính diện tích theo công thức \(S=r^2\cdot pi\)
Xác định bài toán
-Input: Bán kính r
-Output: Diện tích hình tròn có bán kính r
Mô tả thuật toán
-Bước 1: Nhập r
-Bước 2: \(s\leftarrow pi\cdot sqr\left(r\right)\)
-Bước 3: Xuất s
-Bước 4: Kết thúc
Bài 2:
Ý tưởng: Sau khi nhập cạnh a chúng ta sẽ tính chu vi hình vuông có cạnh a theo công thức \(S=4\cdot a\)
Xác định bài toán:
-Input: Cạnh a
-Output: Chu vi hình vuông có cạnh a
Mô tả thuật toán
-Bước 1: Nhập a
-Bước 2: s←a*4;
-Bước 3: Xuất s
-Bước 4: Kết thúc