Giúp mình bài này với mình cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giúp mình với mình cần gấp và mình cần lời giải bài này
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
Trong mp (SAB), từ M kẻ \(MP\perp SB\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp MP\)
\(\Rightarrow MP\perp\left(SBC\right)\Rightarrow MP\in\left(\alpha\right)\)
Trong mp (SBC), qua P kẻ đường thẳng song song MN cắt SC tại Q
\(\Rightarrow NMPQ\) là thiết diện của \(\left(\alpha\right)\) và chóp
\(MN||BC\) (đường trung bình), mà \(BC\perp\left(SAB\right)\Rightarrow MN\perp\left(SAB\right)\Rightarrow MN\perp MP\)
\(\Rightarrow\) Thiết diện là hình thang vuông tại M và P
Từ A kẻ \(AH\perp SB\Rightarrow\) MP là đường trung bình tam giác ABH \(\Rightarrow MP=\dfrac{1}{2}AH\)
Tam giác SAB vuông cân tại A \(\Rightarrow AH=\dfrac{1}{2}SB=\dfrac{1}{2}\sqrt{SA^2+AB^2}=\dfrac{a\sqrt{2}}{2}\Rightarrow MP=\dfrac{a\sqrt{2}}{4}\)
\(MN=\dfrac{BC}{2}=\dfrac{a}{2}\)
\(\dfrac{BP}{BH}=\dfrac{MP}{AH}=\dfrac{1}{2}\Rightarrow BP=\dfrac{1}{2}BH=\dfrac{1}{4}SB\Rightarrow SP=\dfrac{3}{4}SB\)
Talet: \(\dfrac{PQ}{BC}=\dfrac{SP}{SB}=\dfrac{3}{4}\Rightarrow PQ=\dfrac{3}{4}BC=\dfrac{3a}{4}\)
\(S_{NMPQ}=\dfrac{1}{2}MP.\left(MN+PQ\right)=...\)
giúp mình bài này với, mình cần gấp
KV
14 tháng 3 2023
Bán kính hình tròn:
18 : 2 = 9 (cm)
Diện tích hình tròn:
3,14 × 9 × 9 = 254,34 (cm²)
Diện tích hình vuông:
4 × 9 × 9 : 2 = 162 (cm²)
Diện tích phần gạch chéo:
254,34 - 162 = 92,34 (cm²)
14 tháng 3 2023
R=18/2=9cm
=>a=9*2=18cm
\(S_1=18^2=324\left(cm^2\right)\)
\(S_2=9^2\cdot3.14=254.34\left(cm^2\right)\)
Diện tích phần gạch chéo là:
324-254,34=69,66cm2
24 tháng 10 2021
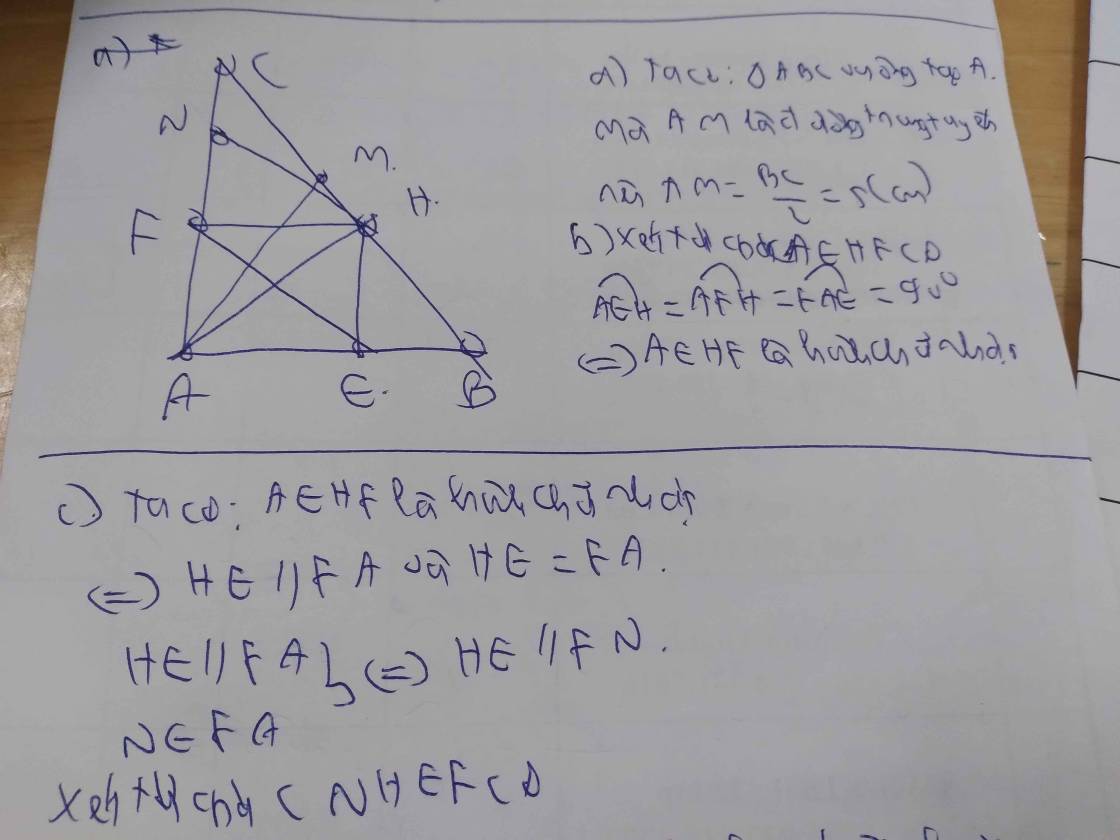
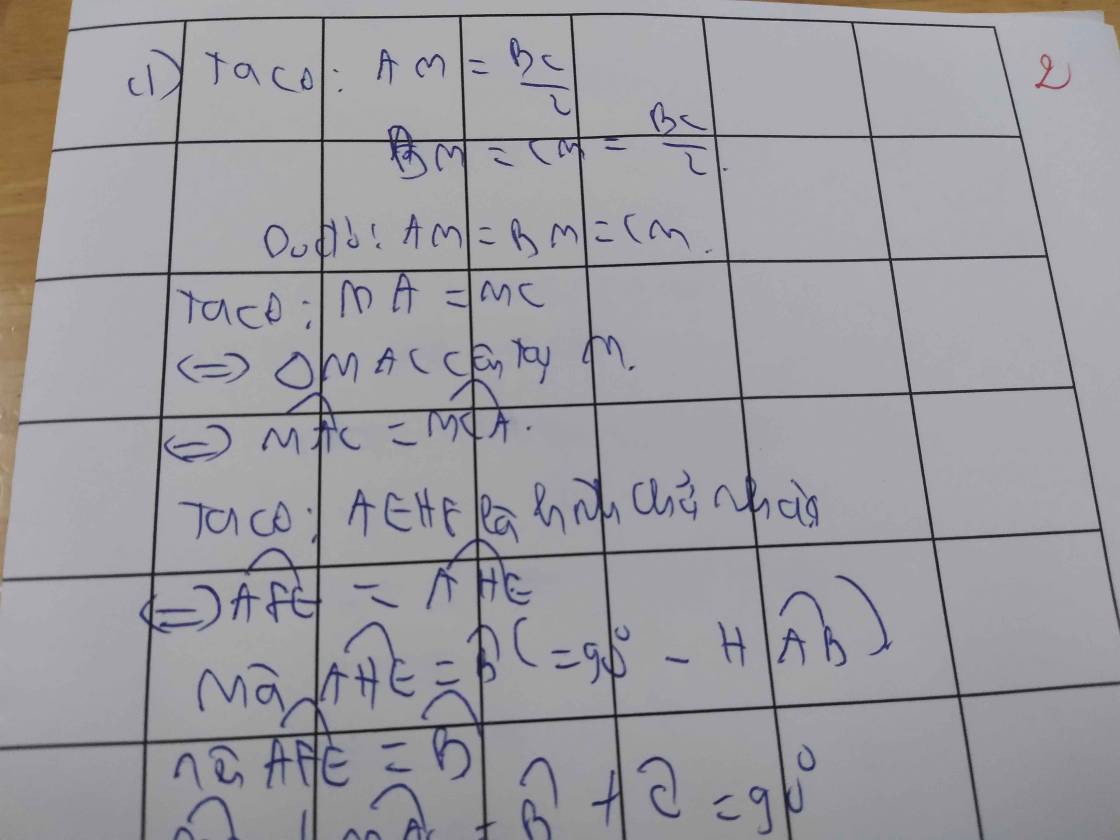
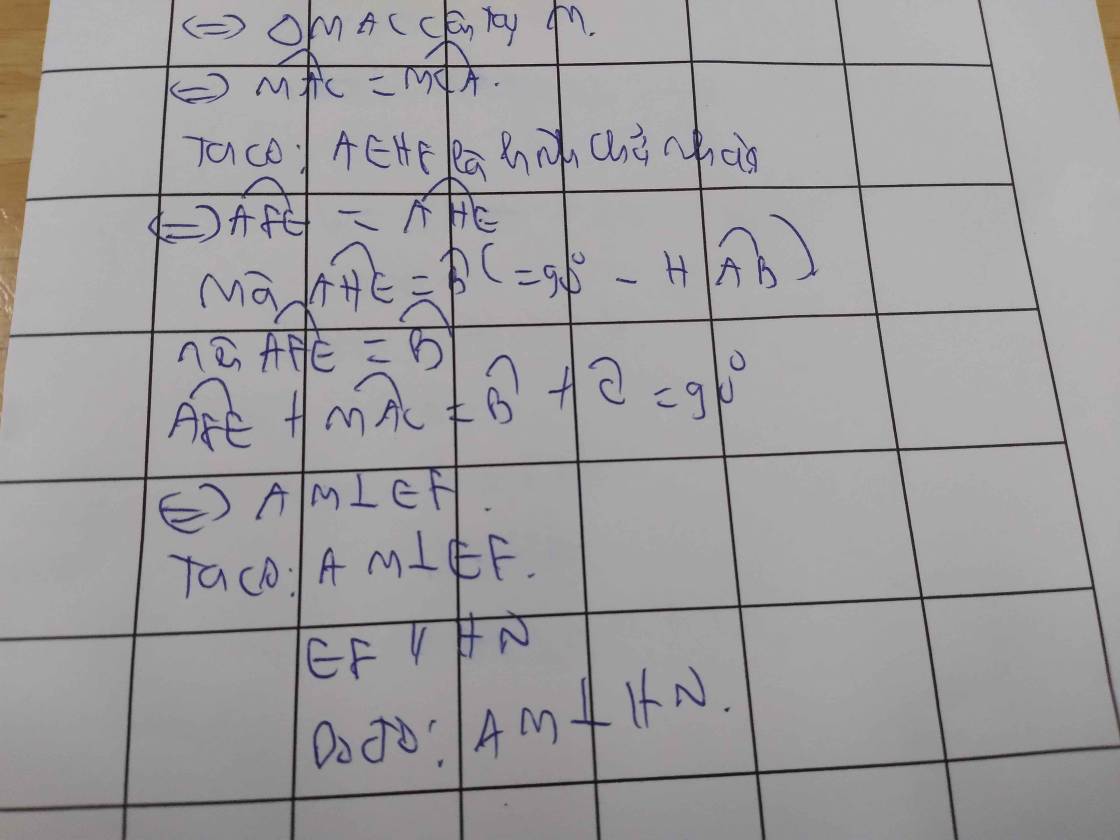
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF
Giúp mình bài này với mình cần gấp ạ
Lời giải:
a.
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$
Xét tam giác $ABC$ có:
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)
$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$
$\Rightarrow \widehat{BAC}=60^0$
b.
Xét tam giác $BAD$ và $EAD$ có:
$AD$ chung
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)
$\widehat{ABD}=\widehat{AED}=90^0$
$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)
c.
Từ tam giác bằng nhau phần b suy ra $AB=AE$
$\Rightarrow ABE$ cân tại $A$
$\Rightarrow \widehat{ABE}=\widehat{AEB}$
Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:
$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$
Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.
Hình vẽ: