Cho tam giác ABC có AB=5cm, AC=7cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD .
a) Tính tỉ số DB/DC và BM/CN
b) CM tam giác AMB đồng dạng tam giác ANC, rồi suy ra AM.DN= AN.DM c) tính SAMB/SANC
d) Qua trung điểm E của BC, Kẻ đường thẳng song song với AD cắt cạnh AC tại P và cắt BA tại Q. Chứng minh BQ=CP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Toán lớp 8 thì mik nghĩ bn vào lazi.vn hoặc hoc.24h.vn để hỏi nha
~ Hok tốt ~
#JH
a)
Xét tam giác ABC ta có
\(AB^2+AC^2=BC^2\)(định lý py ta go)
144 + 256 = BC2
400 = BC2
BC = 20 ( cm )
Xét tam giác ABC có
BD là đường phân giác của tam giác
nên AD/DC = AB/BC = 16/20 = 4/5
có AD + DC = AC = 16
dễ tìm ra AD = 64/9 (cm)
DC = 80/9 (cm)
b) xét 2 tam giác HBA và ABC
có góc ABC chung
2 góc AHB và CAB bằng nhau cùng bằng 90 độ
nên 2 tam giác HAB và ABC đồng dạng với nhau
c)
có 2 tam giác HAB và ABC đồng dạng với nhau
nên \(\frac{S_{HAB}}{S_{ABC}}=\left(\frac{AB}{BC}\right)^2=\left(\frac{12}{20}\right)^2=\frac{9}{25}\)
d)
có E là hình chiếu của của C trên BD
nên \(CE\perp BD\)
suy ra \(\widehat{BEC}=90^0\)
xét 2 tam giác BHK và BEC
có \(\widehat{BHK}=\widehat{BEC}=90^0\)
\(\widehat{CEB}\)chung
nên 2 tam giác BHK và BEC đồng dạng với nhau
suy ra \(\frac{BH}{BE}=\frac{BK}{BC}\Rightarrow BH\cdot BC=BK\cdot BE\)(1)
có 2 tam giác HAB và ABC đồng dạng với nhau
suy ra \(\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH\cdot BC\left(2\right)\)
từ (1) và (2) suy ra
\(AB^2=BK\cdot BE\)

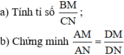
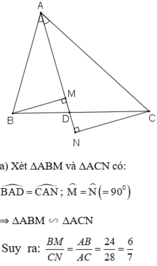


a: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{5}{7}\)
Xét ΔDMB vuông tại M và ΔDNC vuông tại N có
\(\widehat{MDB}=\widehat{NDC}\)(hai góc đối đỉnh)
Do đó: ΔDMB~ΔDNC
=>\(\dfrac{BM}{CN}=\dfrac{DB}{DC}=\dfrac{5}{7}=\dfrac{MB}{NC}\)
b:
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
\(\widehat{BAM}=\widehat{CAN}\)
Do đó:ΔAMB~ΔANC
=>\(\dfrac{AM}{AN}=\dfrac{AB}{AC}\)
mà \(\dfrac{AB}{AC}=\dfrac{DB}{DC}=\dfrac{DM}{DN}\)
nên \(\dfrac{AM}{AN}=\dfrac{DM}{DN}\)
=>\(AM\cdot DN=AN\cdot DM\)
c: ΔAMB~ΔANC
=>\(\dfrac{S_{AMB}}{S_{ANC}}=\left(\dfrac{AB}{AC}\right)^2=\dfrac{25}{49}\)