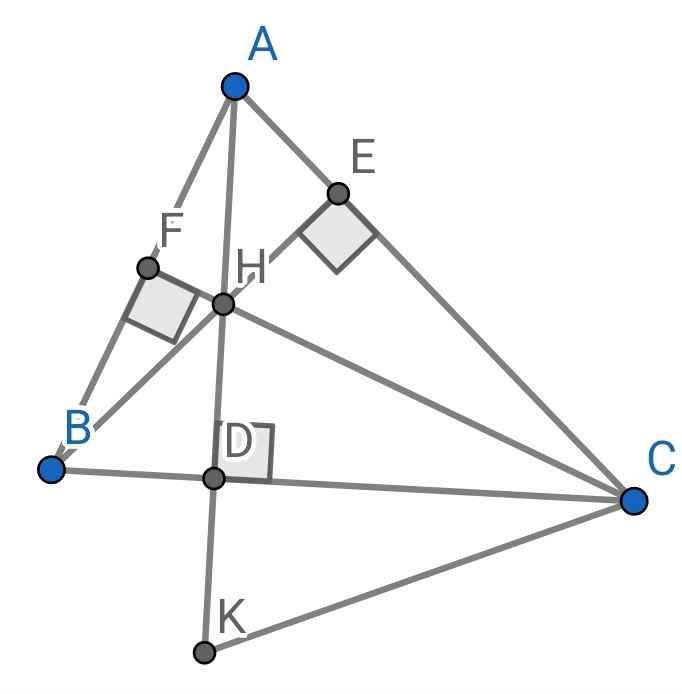
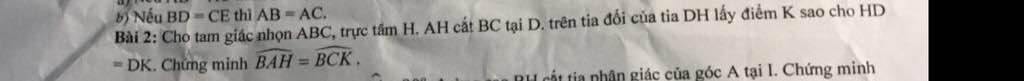 giúp em vẽ hình với ạ
giúp em vẽ hình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)


a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành

( Hình em tự vẽ nhé )
+ Ta có: ΔABC = ΔDEF
=> \(\widehat{A}=\widehat{D}=30^o\)
+ Ta có: \(2\widehat{B}=3\widehat{C}\)
=> \(\widehat{B}=\dfrac{3\widehat{C}}{2}\)
+ Xét ΔABC
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
Mà \(\widehat{A}=30^o;\widehat{B}=\dfrac{3\widehat{C}}{2}\)
=> \(30^o+\dfrac{3\widehat{C}}{2}+\widehat{C}=180^o\)
=> \(\dfrac{3\widehat{C}}{2}+\widehat{C}=150^o\)
\(\Rightarrow\dfrac{3\widehat{C}}{2}+\dfrac{2\widehat{C}}{2}=150^o\)
\(\Rightarrow\dfrac{5\widehat{C}}{2}=150^o\)
\(\Rightarrow5\widehat{C}=75^o\)
\(\Rightarrow\widehat{C}=15^o\)
+ Xét ΔABC
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
\(\Rightarrow30^o+15^o+\widehat{B}=180^o\)
\(\Rightarrow\widehat{B}=135^o\)
Do chị ko có máy ở đây nên ko chụp hình vẽ đc, em thông cảm nhé😢


3:
góc ABC=góc xCB
mà hai góc này ở vị trí so le trong
nên Cx//AB
2:
a: góc AIB và góc CID
góc AID và góc BIC
b: góc BAC và góc ACD
góc ABD và góc BDC
góc DAC và góc ACB
góc BDA và góc DBC
c: góc BAD và góc ADC
góc ABC và góc BCD
góc ADC và góc BCD
góc DAB và góc ABC
d: góc AIB và góc BIC
góc AIB và góc AID

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED

Bài là tam giác vuông hả bạn?
Ta có : BC = BH + CH = \(\sqrt{2}+\sqrt{8}=3\sqrt{2}\)
Xét △ ABC vuông tại A, đường cao AH có:
\(AB^2\)=BH.BC ( hệ thức lượng trong tam giác vuông)
=> \(AB^2=\sqrt{2}.3\sqrt{2}=6\)
=> \(AB=\sqrt{6}\)
\(AC^2=BC.HC\)
=> \(AC^2=\sqrt{8}.3\sqrt{2}=12\)
=>\(AC=2\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.\sqrt{6}.2\sqrt{6}=3\sqrt{2}\left(cm^2\right)\)

+ Góc \(\widehat{AOD}\)
\(\Rightarrow\widehat{AOD}+\widehat{DOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{AOD}+90^O=120^O\)
\(\Rightarrow\widehat{AOD}=120^O-90^O=30^O\)
+ Góc \(\widehat{BOC}\)
\(\Rightarrow\widehat{AOC}+\widehat{COB}=\widehat{AOB}\)
\(\Rightarrow90^O+\widehat{COB}=120^O\)
\(\Rightarrow\widehat{COB}=120^O-90^O=30^O\)
Vậy \(\widehat{AOD}=\widehat{BOC}=30^O\)
Hình vẽ :



 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ





