Cho tam giác MNP. Có MN = MP=5 cm; NP= 5√2. Tính góc M
thanks( nhớ trình bày)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 9 2023
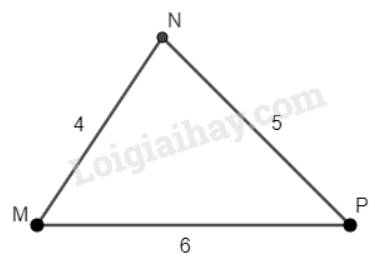
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)
TH
5
22 tháng 3 2019
Ta có:
+ MP2 = 132= 169
+ MN2+NP2= 52+122= 25+144=169
=> MP2 = MN2+NP2 (169=169)
Vậy tam giác MNP vuông tại N (Pytago đảo)
21 tháng 3 2023
a: Xét ΔMNK và ΔMEK có
MN=ME
góc NMK=góc EMK
MK chung
=>ΔMNK=ΔMEK
b,c: Xét ΔKNF và ΔKEP có
KN=KE
góc KNF=góc KEP
NF=EP
=>ΔKNF=ΔKEP
=>KF=KP
d: ΔKNF=ΔKEP
=>góc NKF=góc EKP
=>góc EKP+góc PKF=180 độ
=>F,K,E thẳng hàng
19 tháng 9 2023
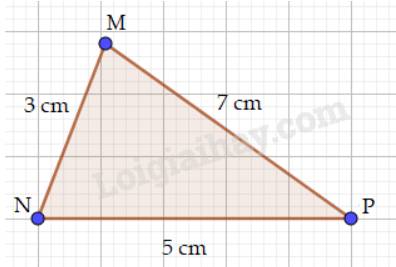
Góc P đối diện với cạnh MN
Góc M đối diện với cạnh NP
Góc N đối diện với cạnh MP.
Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)
Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).
L
9 tháng 3 2020
Bạn tự vẽ hình nha :)
b) Do G và H là trung điểm của NM và MP
=> GH là đường trung bình của tam giác MNP
=> GH // NP và GH = \(\frac{NP}{2}\)
=> GH = \(\frac{4}{2}=2\left(cm\right)\)
Vậy GH = 2 cm
LT
9 tháng 3 2020
Ta có NP2 = 4.4=16
MN2+MP2 = 2,42 + 3,22 = 16
suy ra MN2+MP2=NP2
suy ra tam giác MNP vuông tại M
M N P G H
Vì G là trung điểm của MN, H là trung điểm của MP
suy ra GH = NP : 2 = 2(cm)
30 tháng 4 2022
a: Xét ΔMNP có \(NP^2=MP^2+MN^2\)
nên ΔMNP vuông tại M
b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
\(\widehat{MND}=\widehat{END}\)
DO đó: ΔNMD=ΔNED
Suy ra: DM=DE
28 tháng 3 2022
\(\text{Ta có:MP-MP< MN< MN+MP}\)
\(5-2< MN< 5+2\)
\(3< MN< 7\)
\(\text{Vì NP là 1 số nguyên tố}\)
\(\Rightarrow NP=5\left(cm\right)\)
Ta có: \(NP^2=\left(5\sqrt{2}\right)^2=50\)
\(MN^2+MP^2=5^2+5^2=50\)
Suy ra \(MN^2+MP^2=NP^2\) => tam giác MNP vuông tại M => Góc M = 90o