Chứng minh XZ//OQ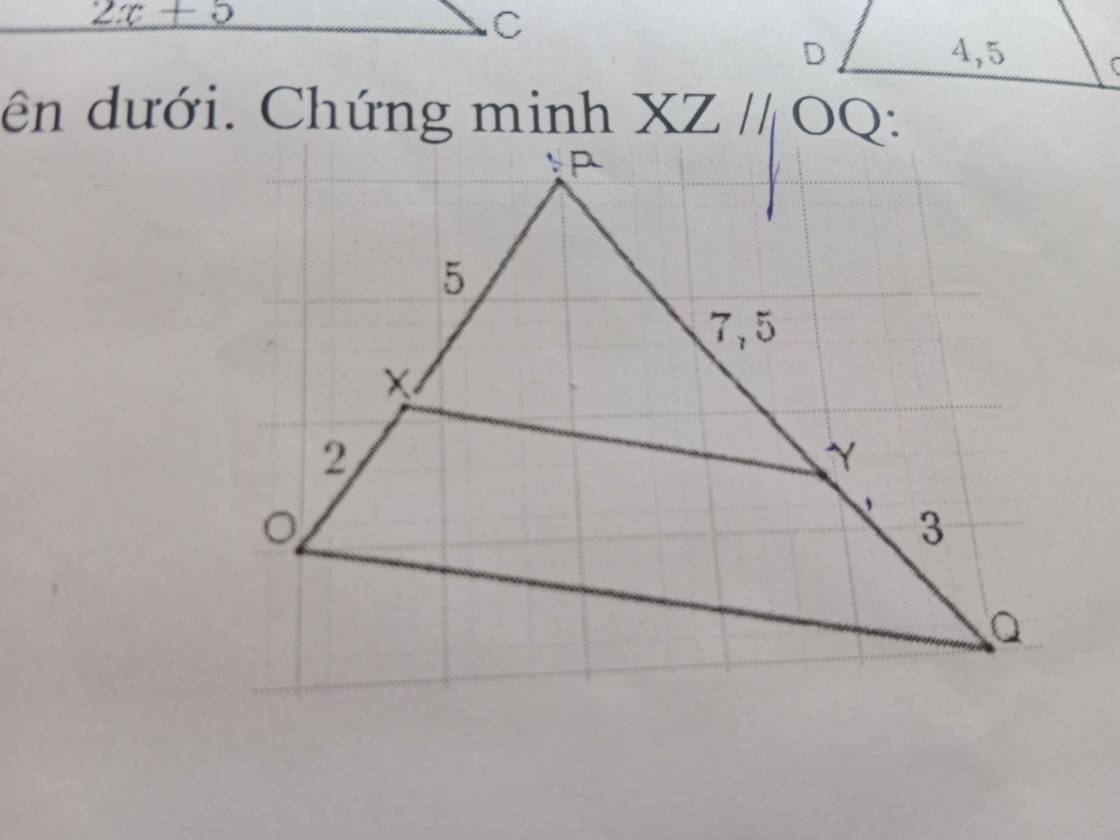
giải giúp em
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
23 tháng 7 2023
Xét ΔMNQ và ΔNMP có
MN chung
NQ=MP
MQ=NP
=>ΔMNQ=ΔNMP
=>góc OMN=góc ONM
=>OM=ON
OM+OP=MP
ON+OQ=NQ
mà MP=NQ và OM=ON
nên OP=OQ
7 tháng 10 2021
1: Xét ΔOPQ có
I là trung điểm của PQ
IN//OP
Do đó: N là trung điểm của OQ
Xét ΔOPQ có
I là trung điểm của PQ
IM//OQ
Do đó: M là trung điểm của OP
Xét ΔMPI và ΔNQI có
MP=NQ
\(\widehat{P}=\widehat{Q}\)
PI=QI
Do đó: ΔMPI=ΔNQI
Suy ra: IM=IN
hay ΔIMN cân tại I
2: Ta có: OM=ON
nên O nằm trên đường trung trực của MN(1)
Ta có: IM=IN
nên I nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OI là đường trung trực của MN
NH
1
HH
2
LH
22 tháng 4 2018
Ta có: \(x-y+z=0\)
\(\Rightarrow\left(x-y+z\right)^2=0
\)
\(\Rightarrow\left(x-y+z\right).\left(x-y+z\right)=0\)
\(\Rightarrow x\left(x-y+z\right)-y\left(x-y+z\right)+z\left(x-y+z\right)=0\)
\(\Rightarrow x^2-xy+xz-xy+y^2-yz+xz-yz+z^2=0\)
\(\Rightarrow x^2+y^2+z^2=xy+xy+yz+yz-xz-xz\)
\(\Rightarrow x^2+y^2+z^2=2xy+2yz-2xz\)
\(\Rightarrow x^2+y^2-z^2=2\left(xy+yz-xz\right)\)
Mà: \(x^2+y^2-z^2\ge0\)
\(\Rightarrow2\left(xy+yz-xz\right)\ge0\)
\(\Rightarrow xy+yz-xz\ge0\)(đpcm)
Vậy: \(xy+yz-xz\ge0\)
NT
giải giúp em bài này và chứng minh A không phải là số tự nhiên. Em cảm ơn ạ!
0
Xét ΔPOQ có \(\dfrac{PX}{XO}=\dfrac{PY}{YQ}\left(\dfrac{5}{2}=\dfrac{7.5}{3}\right)\)
nên XY//OQ