Một hình tam giác ABC có diện tích 180 m2 .Trên cạnh AB lấy điểm N sao cho AN bằng NB; Trên cạnh AC lấy điểm M sao cho AM bằng 2/3AC. Nối N với M.Tính diện tích tam giác ANM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích tam giác ABP bằng 2010÷ 3( vì cùng chiều cao xuata phát từ B với tam giác ABC và đáy AP bằng 1/3 AC). Diện tích tg PMN bằng 1/3 dt tg ABP = 670/3( vì chung đcao xphat từ P và đáy bằng 1/ 3 đáy AB). Dt tg ANC bằng 2/3 dt tg ABC = 1340, dttg NPQ bằng 1/3 dttg ANC = 1340/3. DtMNQP = dttg PMN + NPQ = 670

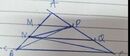

a, - Ta có : \(\left\{{}\begin{matrix}S_{AMD}=\dfrac{1}{2}AM.h\\S_{ADC}=\dfrac{1}{2}AC.h\end{matrix}\right.\)
Mà \(AC=3AM\)
\(\Rightarrow S_{ADC}=3S_{AMD}\)
Lại có : \(\left\{{}\begin{matrix}S_{ABC}=\dfrac{1}{2}BC.h\\S_{ADC}=\dfrac{1}{2}DC.h\end{matrix}\right.\)
Mà \(BC=2DC\)
\(\Rightarrow S_{ABC}=2S_{ADC}=2.3S_{ADM}=6S_{ADM}\)
b, CMTT câu a ta được : \(\left\{{}\begin{matrix}S_{AMN}=\dfrac{1}{6}S_{ABC}\\S_{CMD}=\dfrac{1}{3}S_{ABC}\\S_{BND}=\dfrac{1}{4}S_{ABC}\end{matrix}\right.\)
\(\Rightarrow S_{DMN}=\left(1-\dfrac{1}{6}-\dfrac{1}{3}-\dfrac{1}{4}\right)S_{ABC}=\dfrac{1}{4}S_{ABC}=160\left(cm^2\right)\)

SABCD=1/2(AB+CD)xAH
AB+CD=2xSABCD/AH
=2x36,75/4,2=17,5
mà CD-AB=7,5
CD=12,5;AB=5
Ta có : SADC=1/2AHxCD=1/2x4,2x12,5=26,25
Xét SABC=1/2AHxAB=1/2x4,2x5=10,5
Xét tam giác CAE và tam giác CAD chung đường cao kẻ từ C
Cạnh đáy AE=2/3AD(do AD=3/5DE)
SAEC=2/3SADC=2/3x26,25=17,5
Ta có SAEC - SABC = 17,5-10,5=7dm2
Đáp số : 7 dm2

nối N xuống B ta có hình AMB có diện tích = 1/3 diện tích ABC ( AN= 1/3 AC, chiều cao từ đỉnh B xuống đáy AC.ANM = 2/3 ANB
Nối M với C ta có BMC =1/3 ABC. BMC = ANM
MBQ=1/2 BMC
NCB=2/3 ABC
NQC= 1/2 NCB
ANM = 180: 3 : 3X2 =40 ( cm2)
MBQ = 180 : 3 : 2 = 30 ( cm2 )
NQC = 180 : 3 = 60 ( cm2 )
MNQ= 180 - 40 - 30 - 60 = 50 ( cm2 )
Đ/ S : 50 cm2
( vì không có thời gian nên mình chưa chứng minh phần trên )
Bạn tham khảo
https://olm.vn/hoi-dap/detail/3905646607.html
#NHTP

Vì \(AM=\dfrac{2}{3}AC\)
nên \(S_{ABM}=\dfrac{2}{3}\cdot S_{ABC}=\dfrac{2}{3}\cdot180=120\left(cm^2\right)\)
Vì AN=NB nên N là trung điểm của AB
=>\(AN=\dfrac{1}{2}AB\)
=>\(S_{ANM}=\dfrac{1}{2}\cdot S_{ABM}=\dfrac{1}{2}\cdot120=60\left(cm^2\right)\)