Tam giác ABC vuông tại A, AH là đường cao,AD là phân giác của góc A. Qua D kẻ đường thẳng vuông góc với BC cắt AC tại E. chứng minh BD = DE và suy ra sinBED
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


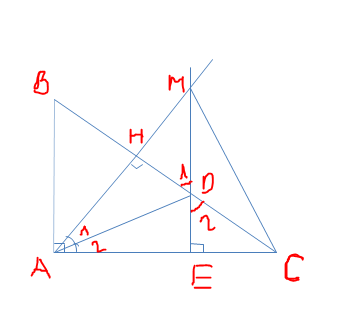
a/ Xét \(\Delta\) vuông AHD và \(\Delta\) AED. Có:
\(\widehat{A1}\)= \(\widehat{A2}\) ( giả thiết)
AD chung
=> \(\Delta AHD=\Delta AED\) ( ch-gn)
=> DH = DE ( 2 cạnh tương ứng )
b/ BMC không cân được bạn nhé. bạn chép nhầm đề bài r: Chứng minh DMC cân mới đúng.
Xét \(\Delta vuôngHDM\) và \(\Delta vuôngEDC\). Có:
\(\widehat{D1}\) = \(\widehat{D2}\) ( đối đỉnh)
HD = HE ( cmt)
=> \(\Delta HDM=\Delta EDC\left(cgv-gnk\right)\)
=> DM = DC ( 2 cạnh tương ứng)
=> Xét \(\Delta DMCcóDM=DC=>\Delta DMCcân\left(cântạiD\right)\)
~ Cậu ktra lại nhé~

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>AD=ED<DC
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
=>BG là trung tuyến

Ta vẽ thêm: Từ điểm D kẻ 2 đường thẳng vuông góc với AB tại H và vuông góc với AC tại K.
Do AD là phân giác của ^BAC=> ^BAD=^DAC. Vì H thuộc AB và K thuộc AC=> ^HAD=^KAD
Xét tam giác ADH và tam giác ADK có:
^AHD=^AKD=90o
Cạnh AD chung => Tam giác ADH = Tam giác ADK ( Cạnh huyền góc nhọn)
^HAD=^KAD
=> DH=DK (2 cạnh tương ứng)
Ta có; Tam giác ABC vuông tại A=> ^ABC+^ACB=90o (2 góc nhọn trong tam giác vuông phụ nhau)
hay: ^HBD+^DCE=90o (Do H thuộc AB, D thuộc BC và E thuộc AC) (1)
Vì DE vuông góc với BC tại D=> Tam giác EDC là tam giác vuông tại D
=> ^DEC+^DCE=90o (phụ nhau) (2)
Từ (1) và (2) => ^HBD+^DCE=^DEC+^DCE=90o => ^HBD=^DEC=90o - ^DCE
Hay có thể nói: ^HBD=^DEK (K thuộc AC)
Xét tam giác BHD: ^BHD+^HBD+^HDB=180o (t/c cộng góc) (3)
Tương tự tam giác EKD: ^EKD+^KED+^EDK=180o (4)
Từ (3) và (4) => ^BHD+^HBD+^HDB=^EKD+^DEK+^EDK=180o (5)
Mà: ^BHD=^EKD=90o ; ^HBD=^DEK (Đã CM) (6)
Từ (5) và (6) => ^HDB=^EDK (Trừ 2 vế cho 2 cặp góc bằng nhau)
Xét tam giác BHD và tam giác EKD:
^BHD=^EKD=90o
DH=DK (CM trên) => Tam giác BHD = Tam giác EKD (g.c.g)
^HDB=^EDK (CM trên)
=> BD=DE (2 cạnh tương ứng) (đpcm)
**** cho mình nha !