Giữa hai tòa nhà (kho và phân xưởng) của một nhà máy người ta xây dựng một băng chuyền AB để nguyên vật liệu. Khoảng cách giữ hai tòa nhà là 10m, còn hai vòng quay của băng chuyển được đặt ở độ cao 8m và 4m so với mặt đất (h.7). Tìm độ dài AB của băng chuyền ?
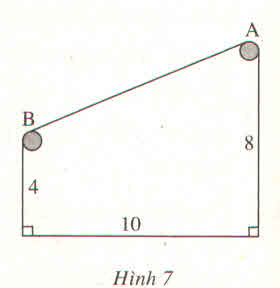

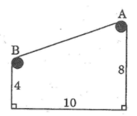
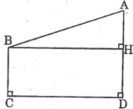
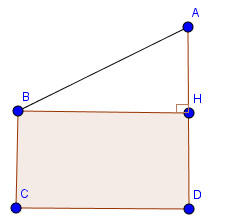


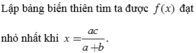
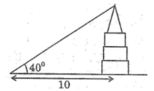






\(AB^2=AH^2+HB^2=10^2+4^2=116\)
\(AB=\sqrt{116}\)