Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng
a: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
=>ΔCAB=ΔCAD
b: Xét ΔMDK và ΔMCB có
góc DMK=góc CMB
MD=MC
góc MDK=góc MCB
=>ΔMDK=ΔMCB
=>DK=CB
BC+BD=BD+DK>BK
a: AB<AC
=>góc C<góc B
b: Xét ΔCBD co
CA vừa là đừog cao, vừa là trung tuyến
=>ΔCBD cân tại C
c: Xét ΔMCB và ΔMDE có
góc MCB=góc MDE
MC=MD
góc CMB=góc DME
=>ΔMCB=ΔMDE
=>BC=DE
`a)` Áp dụng định lý pytago ta có :
`AB^2+AC^2=BC^2`
hay `9^2+12^2=BC^2`
`=>BC^2=225`
`=>BC=15(cm)`
`b)` Xét `ΔABC` và `ΔADC` ta có :
`AC` chung
`\hat{BAC}=90^o`
`\hat{DAC}=90^o`
`=>ΔABC=ΔADC` (c.g.c)
a: Xét ΔCBD co
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
b: Xét ΔMDE và ΔMCB có
góc MDE=góc MCB
MD=MC
góc DME=góc CMB
=>ΔMDE=ΔMCB
=>DE=BC
=>BC+BD=ED+BD>EB
a: Xét ΔCBD có
CA vừa là trung tuyến, vừa là đường cao
=>ΔCDB cân tại C
b: Xét ΔMDE và ΔMCB có
góc DME=góc CMB
MD=MC
góc MDE=góc MCB
=>ΔMDE=ΔMCB
=>ME=MB và CB=DE
BC+BD=ED+BD>BE
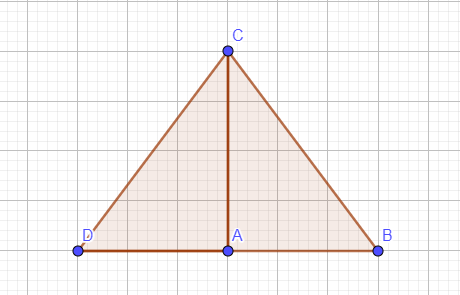
a: Ta có: ΔABC vuông tại A
=>BC là cạnh lớn nhất trong ΔABC
=>BC>AB
b: Xét ΔMBC và ΔMDE có
\(\widehat{MCB}=\widehat{MDE}\)(hai góc so le trong, BC//DE)
MC=MD
\(\widehat{CMB}=\widehat{DME}\)(hai góc đối đỉnh)
Do đó: ΔMBC=ΔMDE
=>DE=BC
Xét ΔEDB có ED+DB>EB
mà ED=BC
nên BC+DB>EB