Hình thang ABCD (AB//CD) có khoảng cách 2 đáy là CH=5m,CD=3,5m và \(\widehat{CDA}=135^o\),\(\widehat{BCH}=30^o\).Tính chu vi và diện tích hình thang ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 3 2021
Định lí 1 : Nếu tam giác vuông có một góc bằng \(30^0\)thì cạnh đối diện với góc ấy bằng nửa cạnh huyền
Vì \(DP\perp AB\)(giả thiết) \(\Rightarrow\Delta PAD\)vuông tại P
\(\Delta PAD\)vuông tại P có \(\widehat{DAP}=60^0\)(giả thiết)
\(\Rightarrow\widehat{PDA}=30^0\)
Do đó \(2PA=DA\)(định lí 1)
\(\Rightarrow4PA^2=DA^2\)
Vì \(\Delta PAD\)vuông tại P (chứng minh trên)
\(\Rightarrow PA^2+PD^2=AD^2\)(định lí Py-ta-go)
\(\Rightarrow PA^2+4^2=4PA^2\)(thay số)
\(\Rightarrow4PA^2-PA^2=16\)
\(\Rightarrow3PA^2=16\)
\(\Rightarrow PA^2=\frac{16}{3}\Rightarrow PA=\sqrt{\frac{16}{3}}=\frac{4}{\sqrt{3}}\left(cm\right)\)(vì \(PA>0\))
Do đó: \(DA=2PA=2.\frac{4}{\sqrt{3}}=\frac{8}{\sqrt{3}}\left(cm\right)\)
Vì \(CH\perp AB\)(giả thiết)
\(\Rightarrow\Delta CHB\)vuông tại H.
\(\Delta CHB\)vuông tại H có \(\widehat{HCB}=60^0\)(giả thiết)
\(\Rightarrow BC=2HC\)(định lí 1)
\(\Rightarrow BC=2.4\)(thay số)
\(\Rightarrow BC=8\left(cm\right)\)
Vì \(\Delta CHB\)vuông tại H (chứng minh trên)
\(\Rightarrow HB^2+HC^2=BC^2\)(định lí Py-ta-go)
\(\Rightarrow HB^2+4^2=8^2\)(thay số)
\(\Rightarrow HB^2+16=64\)
\(\Rightarrow HB^2=56\Rightarrow HB=\sqrt{56}=2\sqrt{14}\left(cm\right)\)(vì \(HB>0\))
Mặt khác, xét tứ giác DCHP có:
\(DP//CH\)(vì cùng vuông góc với AB)
Và \(DP=CH\)(giả thiết)
\(\Rightarrow\)DCHP là hình bình hành
\(\Rightarrow CD=PH=3\left(cm\right)\)(tính chất).
Ta có:
\(AB=AP+PH+HB\)
\(\Rightarrow AB=\frac{4}{\sqrt{3}}+3+2\sqrt{14}\left(cm\right)\)
Do đó:
\(P_{ABCD}=AB+BC+CD+DA=\)\(\frac{4}{\sqrt{3}}+3+2\sqrt{14}+8+3+\frac{8}{\sqrt{3}}\)(thay số)
\(P_{ABCD}=\frac{12}{\sqrt{3}}+14+2\sqrt{14}=4\sqrt{3}+2\sqrt{14}+14\left(cm\right)\)
Vậy \(P_{ABCD}=4\sqrt{3}+2\sqrt{14}+14\left(cm\right)\)
4 tháng 9 2018
Kẻ \(BH\perp CD\)
Mà \(CD\perp AD\left(gt\right)\Rightarrow BH//AD\)
Hình thang ABHD (AB//HD) có BH//AD nên \(\hept{\begin{cases}HD=AB=5\left(cm\right)\\BH=AD\end{cases}}\) (t/c hình thang)
\(HD+HC=DC\Rightarrow5+HC=9\Rightarrow HC=4\left(cm\right)\)
\(\Delta HBC\)vuông cân tại H nên \(HB=HC=4cm\Rightarrow AD=4cm\left(AD=BH\right)\)
Áp dụng định lí Pitago tính được \(BC=\sqrt{32}\left(cm\right)\)
Chu vi hình thang vuông ABCD là:
\(AB+BC+CD+AD=5+\sqrt{32}+9+4=18+\sqrt{32}\left(cm\right)\)
Chúc bạn học tốt.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
11 tháng 3 2019
Trong hình thang ABCD đường cao hạ từ A xuống CD = đường cao hạ từ C xuống AB
Xét tam giác ACD và tam giác ABC, hai tam giác này có đường cao hạ từ A xuống CD và đường cao hạ từ C xuống AB băng nhau nên
\(\frac{S_{ABC}}{S_{ACD}}=\frac{AB}{CD}=\frac{1}{3}\Rightarrow S_{ACD}=3xS_{ABC}=3x36=108cm^2\)
\(\Rightarrow S_{ABCD}=S_{ABC}+S_{ACD}=36+108=144cm^2\)
9 tháng 7 2023
a: góc A-góc D=20 độ
góc A+góc D=180 độ
=>góc A=(20+180)/2=100 độ và góc D=180-100=80 độ
góc B=2*góc C
góc B+góc C=180 độ
=>góc B=2/3*180=120 độ; góc C=180-120=60 độ
b: góc B-góc C=20 độ
góc B+góc C=180 độ
=>góc B=(180+20)/2=100 độ và góc C=80 độ
=>góc A=100+20=120 độ
=>góc D=60 độ
A
21 tháng 1 2021
Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2
21 tháng 1 2021
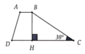
Kẻ BH \(\perp\) CD tại H
Xét tam giác BHC vuông tại H (BH \(\perp\) CD): \(\widehat{C}\) = 30o
\(\Rightarrow\) BH = \(\dfrac{1}{2}\)BC (Tính chất cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
hay BH = \(\dfrac{1}{2}\).8 = 4(cm)
Vì ABCD là hình thang (AB // CD)
\(\Rightarrow\) SABCD = \(\dfrac{1}{2}\)(AB + CD).BH = \(\dfrac{1}{2}\).(2 + 9).4 = 22 (cm2)
Chúc bn học tốt!
Hạ AJ vuông góc CD mọi vấn đề đ.c giải quyết =))