Question

[BÙI BẢO KHÁNH]

Bài 1:Cho A = n-7/n-4(nϵZ)

1.Tìm điều kiện của số nguyên n để A là phân số.

2,Tìm các giá trị nguyên của n để A là số nguyên.

Bài 2: So sánh các phân số sau:

1, 2009.2010-1/2009.2010 và 2010.2011-1/2010.2011;(HD:dùng phần bù)

2,377.733+722/379.733-744 và 1;(HD:377.733+722/379.733-744=377.733+733-11/379.733-733-11)

3,579.933-944/577.933+922 và 1

4,A=10 mũ 17 + 1/10 mũ 18 + 1 và B=10 mũ 18+1/10 mũ 19 +1

5,A=10 mũ 12 + 1/10 mũ 11 + 1 và B = 10 mũ 2011 + 1/10 mũ 2010 + 1

6,A=10 mũ 2012 + 1/10 mũ 2013 + 1 và B= 10 mũ 2013 + 1/10 mũ 2014 + 1

ALOOOOOO,CÁC THIÊN TÀI HỌC TOÁN ĐÂU RỒI,VÀO ĐÂY GIÚP MÌNH VS Ạ,HELP MEEEE!!!!!!!!!!!

Answer 1

[Nguyễn Thị Thương Hoài]

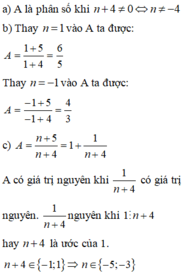
Bài 1:

a; A = \(\dfrac{n-7}{n-4}\) (n \(\in\) Z)

A là phân số ⇔ n \(\in\) Z; n - 4 ≠ 0 ⇒ n ≠ 4

Vậy A là phân số khi  4 ≠ n \(\in\) Z

b; A \(\in\) Z ⇔ n - 7 ⋮ n - 4

            n - 4 - 3  ⋮ n - 4

                      3 ⋮ n - 4

  n - 4 \(\in\) Ư(3) = {-3; -1; 1; 3}

Lập bảng ta có:

n-4	-3	-1	1	3
n	1	3	5	7

Theo bảng trên ta có n \(\in\) {1; 3; 5; 7}

Vậy n \(\in\) {1; 3; 5; 7}

Answer 2

[Nguyễn Thị Thương Hoài]

Bài 2: 

1;    \(\dfrac{2009.2010-1}{2009.2010}\) 

  = \(\dfrac{2009.2010}{2009.2010}-\dfrac{1}{2009.2010}\)

  =  1 - \(\dfrac{1}{2009.2010}\)

\(\dfrac{2010.2011-1}{2010.2011}\)

= \(\dfrac{2010.2011}{2010.2011}-\dfrac{1}{2010.2011}\)

 = 1  - \(\dfrac{1}{2010.2011}\)

Vì \(\dfrac{1}{2009.2010}>\dfrac{1}{2010.2011}\)

Vậy \(\dfrac{2009.2010-1}{2009.2010}< \dfrac{2010.2011-1}{2010.2011}\)