Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,\(A=\frac{1}{5}+\frac{1}{5^2}+\frac{1}{5^3}+...+\frac{1}{5^{100}}\)
\(=>5A=1+\frac{1}{5}+\frac{1}{5^2}+...+\frac{1}{5^{99}}\)
\(=>5A-A=1-\frac{1}{5^{100}}=>A=\frac{1-\frac{1}{5^{100}}}{4}\)
b, Ta có \(1-\frac{1}{5^{100}}< 1=>\frac{1-\frac{1}{5^{100}}}{4}< \frac{1}{4}\)hay \(A< \frac{1}{4}\)


2)Ta có: \(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì \(8^{111}< 9^{111}\) mà \(2^{332}< 8^{111},3^{223}>9^{111}\) nên suy ra \(2^{332}< 3^{223}\)
Vậy \(2^{332}< 3^{223}\)
1) \(A=\dfrac{10^{2013}+1}{10^{2014}+1}\Rightarrow10A=\dfrac{10^{2014}+10}{10^{2014}+1}=\dfrac{10^{2014}+1}{10^{2014}+1}+\dfrac{9}{10^{2014}+1}=1+\dfrac{9}{10^{2014}+1}\)
\(B=\dfrac{10^{2014}+1}{10^{2015}+1}\Rightarrow10B=\dfrac{10^{2015}+10}{10^{2015}+1}=\dfrac{10^{2015}+1}{10^{2015}+1}+\dfrac{9}{10^{2015}+1}=1+\dfrac{9}{10^{2015}+1}\)Vì: \(10^{2014}+1< 10^{2015}+1\Rightarrow\dfrac{9}{10^{2014}+1}>\dfrac{9}{10^{2015}+1}\Rightarrow1+\dfrac{9}{10^{2014}+1}>1+\dfrac{9}{10^{2015}+1}\)
Nên suy ra \(10A>10B\Rightarrow A>B\)

Đặt \(a=10^5\)
Theo đề bài ta có:
\(A=\frac{a+4}{a-1};B=\frac{a+3}{a-2}\)
Ta thấy a+4 và a-1 2 số này có tử và mẫu chênh lệch nhiều hơn a+3 và a-2 Nên A>B
Bạn tự suy luận có thể ra ngay thôi

Giải:
Ta có:
A=2010+1/2010-1
A=2010-1+2/2010-1
A=1+2/2010-1
Tương tự:
B=2010-1/2010-3
B=2010-3+2/2010-3
B=1+2/2010-3
Vì 2/2010-1<2/2010-3 nên A<B
Chúc bạn học tốt!

Mình làm câu a) nha!!!
+) \(A=2009^{2010}+2009^{2009}\)
\(=2009^{2009}.\left(2009+1\right)\)
\(=2009^{2009}.2010\)
+) \(B=2010^{2010}=2010^{2009}.2010\)
Vì \(2010^{2009}>2009^{2009}\)nên \(2010^{2009}.2010>2009^{2009}.2010\)hay \(B>A\)
Vậy \(A< B\)
Hok tốt nha^^


\(A=\dfrac{10^{11}+1}{10^{12}-1}\)
\(\Rightarrow10A=\dfrac{10^{11}+1}{10^{12}-1}.10\)
\(\Rightarrow10A=\dfrac{10\left(10^{11}+1\right)}{10^{12}-1}\)
\(\Rightarrow10A=\dfrac{10^{12}-10}{10^{12}-1}\)
\(B=\dfrac{10^{10}+1}{10^{11}+1}\)
\(\Rightarrow10B=\dfrac{10^{10}+1}{10^{11}+1}.10\)
\(\Rightarrow10B=\dfrac{\left(10^{10}+1\right).10}{10^{11}+1}\)
\(\Rightarrow10B=\dfrac{10^{11}+10}{10^{11}+1}\)
Ta thấy:
\(10^{12}-1>10^{12}-10>0\Rightarrow10A< 1\)
\(0< 10^{11}+1< 10^{11}+10\Rightarrow10B>1\)
Mà \(10A< 1;10B>1\)
\(\Rightarrow B>A\).
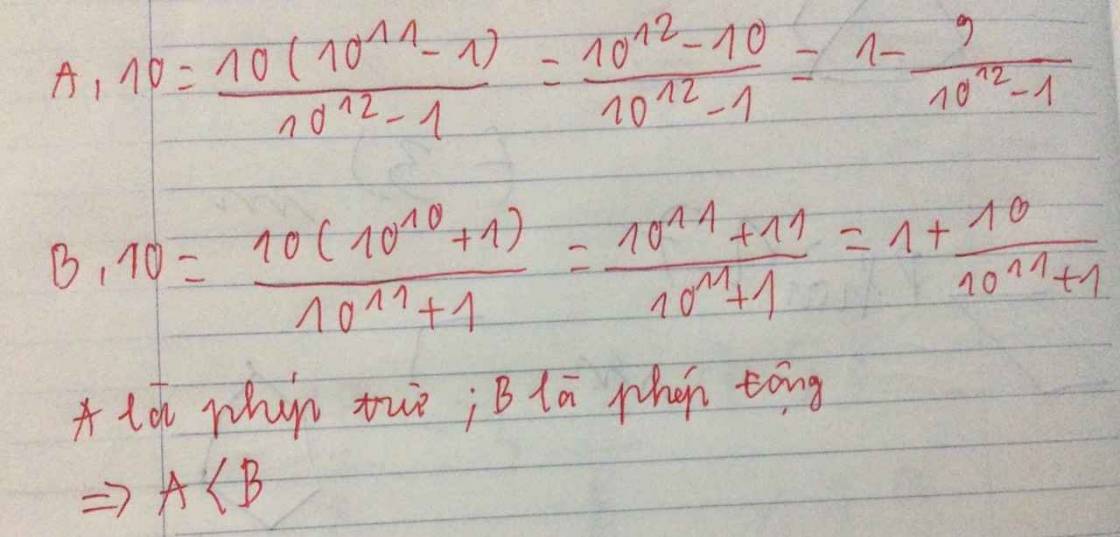
A là bằng nhau
B là >