Mong các bạn giúp,tớ cần gấp!
Cho C nằm ngoài đường tròn tâm O.Kẻ tiếp tuyến CA,CB với đường tròn tâm O ( A,B là tiếp điểm).Cát tuyết CDE ( D nằm giữa C và E).Gọi I là trung điểm DE, H là giao điểm AB và OC.
a) C/m 5 điểm C,A,I,O,B cùng thuộc 1 đường tròn.
b) C/m AH^2 = OH.HC = AB^2/4 và CH.CO = CI^2 - DI^2
c) C/m đường tròn ngoại tiếp tam giác DEH luôn đi qua điểm cố định.


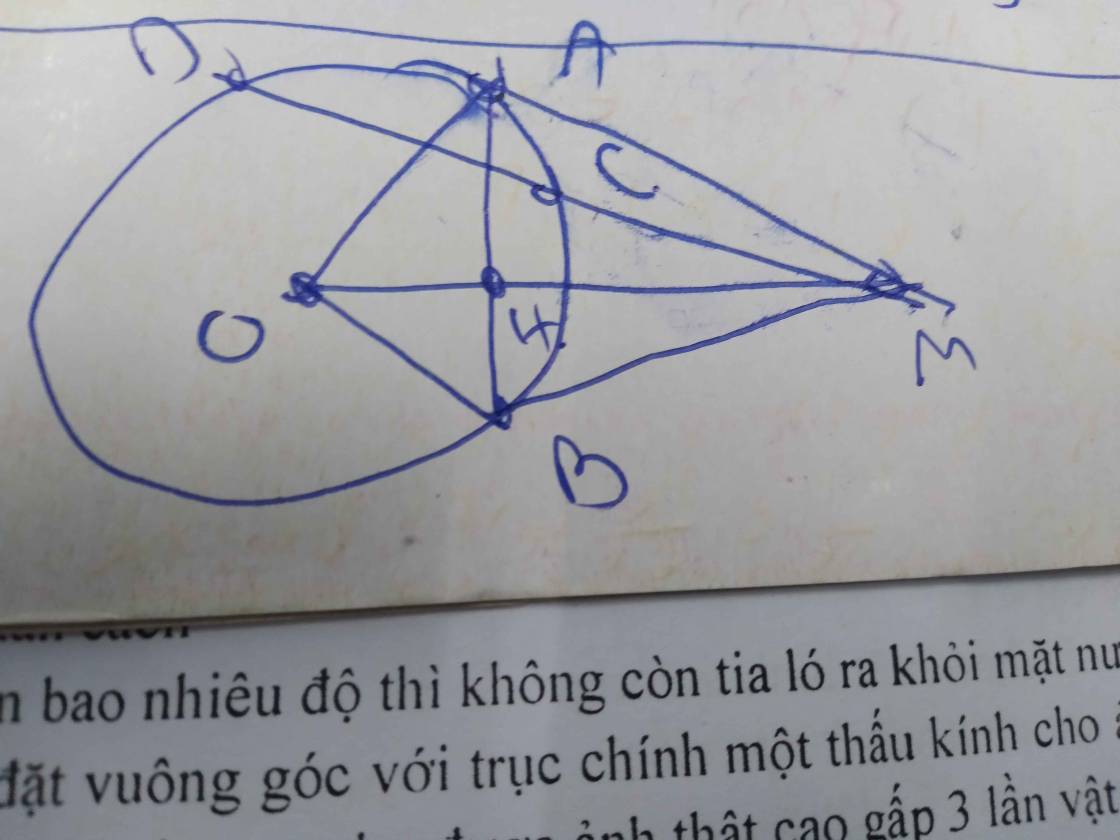


a: Ta có: ΔOED cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)ED
Ta có: \(\widehat{OIC}=\widehat{OAC}=\widehat{OBC}=90^0\)
=>O,I,C,A,B cùng thuộc đường tròn đường kính OC
b: Xét (O) có
CA,CB là các tiếp tuyến
Do đó: CA=CB
=>C nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OC là đường trung trực của AB
=>OC\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAC vuông tại A có AH là đường cao
nên \(AH^2=OH\cdot HC\)
=>\(OH\cdot HC=AH^2=\left(\dfrac{1}{2}AB\right)^2=\dfrac{1}{4}AB^2\)
Xét (O) có
\(\widehat{CAD}\) là góc tạo bởi tiếp tuyến AC và dây cung AD
\(\widehat{AED}\) là góc nội tiếp chắn cung AD
Do đó: \(\widehat{CAD}=\widehat{AED}\)
=>\(\widehat{CAD}=\widehat{CEA}\)
Xét ΔCAD và ΔCEA có
\(\widehat{CAD}=\widehat{CEA}\)
\(\widehat{ACD}\) chung
Do đó: ΔCAD~ΔCEA
=>\(\dfrac{CA}{CE}=\dfrac{CD}{CA}\)
=>\(CD\cdot CE=CA^2\)
\(CI^2-DI^2=\left(CI-DI\right)\cdot\left(CI+DI\right)\)
\(=CD\cdot CE=CA^2\left(3\right)\)
Xét ΔOAC vuông tại A có AH là đường cao
nên \(CH\cdot CO=CA^2\left(4\right)\)
Từ (3) và (4) suy ra \(CI^2-DI^2=CH\cdot CO\)
c: Ta có: CD*CE=CH*CO
=>\(\dfrac{CD}{CO}=\dfrac{CH}{CE}\)
Xét ΔCDH và ΔCOE có
\(\dfrac{CD}{CO}=\dfrac{CH}{CE}\)
\(\widehat{DCH}\) chung
Do đó: ΔCDH~ΔCOE
=>\(\widehat{CDH}=\widehat{COE}\)
mà \(\widehat{CDH}+\widehat{EDH}=180^0\)(hai góc kề bù)
nên \(\widehat{EDH}+\widehat{EOH}=180^0\)
=>EDHO là tứ giác nội tiếp
=>ĐƯờng tròn ngoại tiếp ΔDEH luôn đi qua O cố định