Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có AC ; AB lần lượt là tiếp tuyến (O) với C;B là tiếp điểm
=> ^ACO = ^ABO = 900
Xét tứ giác ABOC có
^ACO + ^ABO = 1800
mà 2 góc này đối
Vậy tứ giác ABOC là tứ giác nt 1 đường tròn
hay các điểm A;B;O;C cùng thuộc 1 đường tròn
b, Ta có AB = AC ( tc tiếp tuyến cắt nhau )
OC = OB = R
Vậy OA là đường trung trực đoạn BC
=> OA vuông BC
Xét tam giác ACO vuông tại C, đường cao CH
Ta có AC^2 = AH.AO ( hệ thức lượng )
Xét tam giác ACE và tam giác ADC
^A _ chung
^ACE = ^ADC ( cùng chắn cung CE )
Vậy tam giác ACE ~ tam giác ADC (g.g)
\(\dfrac{AC}{AD}=\dfrac{AE}{AC}\Rightarrow AC^2=AE.AD\)
=> AH . AO = AE . AD (*)
Xét tam giác AHE và tam giác ADO ta có
AH/AD = AE/AO ( tỉ lệ thức * )
^A _ chung
Vậy tam giác AHE ~ tam giác ADO (g.g)
=> ^AHE = ^ADO (1)
Lại có ^ACE = ^CDE ( cùng chắn cung CE ) (2)
Lấy (1) + (2) ta được ^BDC = ^AHE + ^ACE
dm có ông nào giải hộ tôi điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii

Lời giải 1 bài toán tương tự - Dài và khó
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube
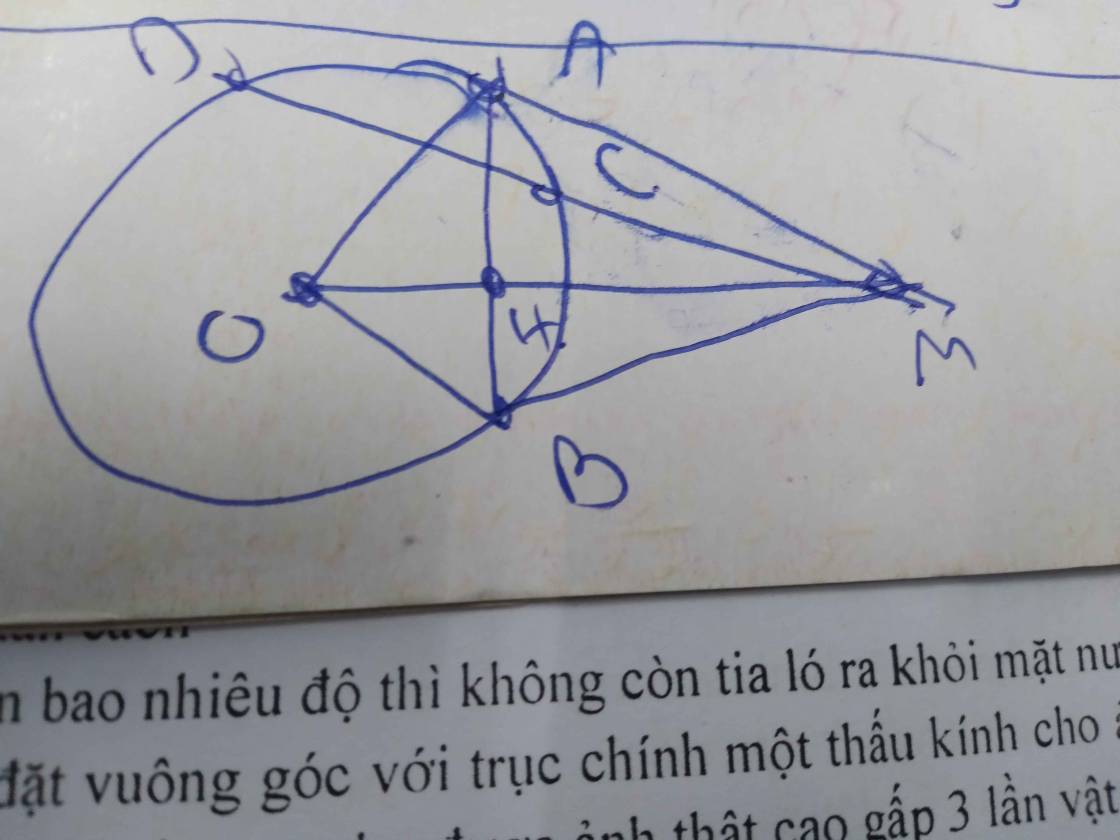


a: Ta có: ΔOED cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)ED
Ta có: \(\widehat{OIC}=\widehat{OAC}=\widehat{OBC}=90^0\)
=>O,I,C,A,B cùng thuộc đường tròn đường kính OC
b: Xét (O) có
CA,CB là các tiếp tuyến
Do đó: CA=CB
=>C nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OC là đường trung trực của AB
=>OC\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAC vuông tại A có AH là đường cao
nên \(AH^2=OH\cdot HC\)
=>\(OH\cdot HC=AH^2=\left(\dfrac{1}{2}AB\right)^2=\dfrac{1}{4}AB^2\)
Xét (O) có
\(\widehat{CAD}\) là góc tạo bởi tiếp tuyến AC và dây cung AD
\(\widehat{AED}\) là góc nội tiếp chắn cung AD
Do đó: \(\widehat{CAD}=\widehat{AED}\)
=>\(\widehat{CAD}=\widehat{CEA}\)
Xét ΔCAD và ΔCEA có
\(\widehat{CAD}=\widehat{CEA}\)
\(\widehat{ACD}\) chung
Do đó: ΔCAD~ΔCEA
=>\(\dfrac{CA}{CE}=\dfrac{CD}{CA}\)
=>\(CD\cdot CE=CA^2\)
\(CI^2-DI^2=\left(CI-DI\right)\cdot\left(CI+DI\right)\)
\(=CD\cdot CE=CA^2\left(3\right)\)
Xét ΔOAC vuông tại A có AH là đường cao
nên \(CH\cdot CO=CA^2\left(4\right)\)
Từ (3) và (4) suy ra \(CI^2-DI^2=CH\cdot CO\)
c: Ta có: CD*CE=CH*CO
=>\(\dfrac{CD}{CO}=\dfrac{CH}{CE}\)
Xét ΔCDH và ΔCOE có
\(\dfrac{CD}{CO}=\dfrac{CH}{CE}\)
\(\widehat{DCH}\) chung
Do đó: ΔCDH~ΔCOE
=>\(\widehat{CDH}=\widehat{COE}\)
mà \(\widehat{CDH}+\widehat{EDH}=180^0\)(hai góc kề bù)
nên \(\widehat{EDH}+\widehat{EOH}=180^0\)
=>EDHO là tứ giác nội tiếp
=>ĐƯờng tròn ngoại tiếp ΔDEH luôn đi qua O cố định