Giải phương trình:
(x + 1)(x2 + x + 1) = (x + 1)[(x + 1)2 - 1]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(\left(9x^2-4\right)\left(x+1\right)=\left(3x+2\right)\left(x^2-1\right)\)
\(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)=\left(3x+2\right)\left(x+1\right)\left(x-1\right)\)
\(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[9x^2-4-\left[\left(3x+2\right)\left(x-1\right)\right]\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left[9x^2-4-\left(3x^2-3x+2x-2\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+3x-2x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(6x^2+x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\6x^2+x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(2x-1\right)\left(3x+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{1;\dfrac{-2}{3};\dfrac{1}{2}\right\}\)
b)
\(\left(x-1\right)^2-1+x^2=\left(1-x\right)\left(x+3\right)\)
\(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow x=\left(\pm1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy \(x\in\left\{1;-1\right\}\)

1) `x^2+4-2(x-1)=(x-2)^2`
`<=>x^2+4-2x+2=x^2-4x+4`
`<=>-2x+2=-4x`
`<=>2x=-2`
`<=>x=-1`
.
2) ĐKXĐ: `x \ne \pm 3`
`(x+3)/(x-3)-(x-1)/(x+3)=(x^2+4x+6)/(x^2-9)`
`<=>(x+3)^2-(x-1)(x-3)=x^2+4x+6`
`<=>x^2+6x+9-x^2+4x-3=x^2+4x+6`
`<=>10x+6=x^2+4x+6`
`<=>x^2-6x=0`
`<=>x(x-6)=0`
`<=>x=0;x=6`
.
3) ĐKXĐ: `x \ne \pm 3`
`(3x-3)/(x^2-9) -1/(x-3 )= (x+1)/(x+3)`
`<=>(3x-3)-(x+3)=(x+1)(x-3)`
`<=> 2x-6=x^2-2x-3`
`<=>x^2-4x+3=0`
`<=>x^2-x-3x+3=0`
`<=>x(x-1)-3(x-1)=0`
`<=>(x-3)(x-1)=0`
`<=> x=3;x=1`
Vậy...

a: =>x-3=2 hoặc x-3=-2
=>x=5 hoặc x=1
b: =>x2=0
hay x=0
c: =>(3x-5-x+1)(3x-5+x-1)=0
=>(2x-4)(4x-6)=0
=>x=2 hoặc x=3/2
d: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(2x-1-x-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-4\right)=0\)
hay \(x\in\left\{1;-1;4\right\}\)
\(a,\left(x-3\right)^2=4\\\Leftrightarrow\left(x-3\right)^2-2^2=0\\ \Leftrightarrow \left(x-3-2\right).\left(x-3+2\right)=0\\ \Leftrightarrow\left(x-5\right).\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\\\Rightarrow S=\left\{1;5\right\}\\ b,x^2.\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2=0\\x^2+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=-1\left(vô.lí\right)\end{matrix}\right.\\ \Rightarrow S=\left\{0\right\}\\ c,\left(3x-5\right)^2-\left(x-1\right)^2=0\\ \Leftrightarrow\left(3x-5-x+1\right).\left(3x-5+x-1\right)=0\\ \Leftrightarrow\left(2x-4\right).\left(4x-6\right)=0\\ \Leftrightarrow2.\left(x-2\right).2.\left(2x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{3}{2}\end{matrix}\right.\\ \Rightarrow S=\left\{\dfrac{3}{2};2\right\}\)
\(d,\left(x^2-1\right).\left(2x-1\right)=\left(x^2-1\right).\left(x+3\right)\\ \Leftrightarrow\left(x^2-1\right).\left(2x-1-x-3\right)=0\\ \Leftrightarrow\left(x^2-1\right).\left(x-4\right)=0\\ \Leftrightarrow\left(x-1\right).\left(x+1\right).\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=4\end{matrix}\right.\\ \Rightarrow S=\left\{-1;1;4\right\}\)

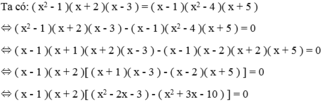
⇔ ( x - 1 )( x + 2 )( 7 - 5x ) = 0
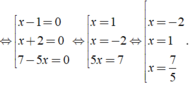
Vậy phương trình có tập nghiệm là S = { - 2; 1; 7/5 }.

\(a,\left(2x-3\right)^2=\left(x+1\right)^2\\ \Leftrightarrow\left(2x-3\right)^2-\left(x+1\right)^2=0\\ \Leftrightarrow\left(2x-3+x+1\right)\left(2x-3-x-1\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(x-4\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=2\\x=4\end{matrix}\right. \\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=4\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{2}{3};4\right\}\)
\(b,x^2-6x+9=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2-9\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-3^2\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left[3\left(x-1\right)\right]^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left(3x-3\right)^2=0\\ \Leftrightarrow\left(x-3+3x-3\right)\left(x-3-3x+3\right)=0\\ \Leftrightarrow-2x\left(4x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-2x=0\\4x-6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\4x=6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{0;\dfrac{3}{2}\right\}\)

a) Ta có: (1) ⇔ |x + 1|2 = | x – 1|2 ⇔ (x + 1)2 = (x – 1)2
⇔ (x + 1)2 – (x – 1)2 = 0 ⇔ (x + 1 + x – 1)(x + 1 – x + 1) = 0
⇔ 4x = 0 ⇔ x = 0
Tập nghiệm: S = {0}.
b) Trường hợp 1: x ≥ 0.
Khi đó (2) ⇔ 4x = x2 + 4 ⇔ x2 – 4x + 4 = 0
⇔ (x – 2)2 = 0 ⇔ x = 2 ( thỏa điều kiện x ≥ 0)
Trường hợp 2: x < 0.
Khi đó (2) ⇔ –4x = x2 + 4 ⇔ x2 + 4x + 4 = 0
⇔ (x + 2)2 = 0 ⇔ x = –2 ( thỏa mãn điều kiện x > 0)
Tập nghiệm: S = {–2; 2}.
Bài 1: Giải các bất phương trình sau
a) x+1/x+3 > 1
b) 2x-1/x-3 ≤ 2
c) x2+2x+2/x2+3 ≥ 1
d) 2x+1/x2+2 ≥ 1

a, \(\dfrac{x+1}{x+3}>1\Leftrightarrow\dfrac{x+1}{x+3}-1>0\Leftrightarrow\dfrac{x+1-x-3}{x+3}>0\)
\(\Rightarrow x+3< 0\)do -2 < 0
\(\Rightarrow x< -3\)Vậy tập nghiệm BFT là S = { x | x < -3 }
b, \(\dfrac{2x-1}{x-3}\le2\Leftrightarrow\dfrac{2x-1}{x-3}-2\le0\Leftrightarrow\dfrac{2x-1-2x+6}{x-3}\le0\)
\(\Rightarrow x-3\le0\)do 5 > 0
\(\Rightarrow x\le3\)Vậy tập nghiệm BFT là S = { x | x \(\le\)3 }
c, \(\dfrac{x^2+2x+2}{x^2+3}\ge1\Leftrightarrow\dfrac{x^2+2x+2}{x^2+3}-1\ge0\)
\(\Leftrightarrow\dfrac{x^2+2x+2-x^2-3}{x^2+3}\ge0\Rightarrow2x-1\ge0\)do x^2 + 3 > 0
\(\Rightarrow x\ge\dfrac{1}{2}\)Vậy tập nghiệm BFT là S = { x | x \(\ge\)1/2 }
mình ko chắc nên mình đăng sau :>
d, \(\dfrac{2x+1}{x^2+2}\ge1\Leftrightarrow\dfrac{2x+1}{x^2+2}-1\ge0\Leftrightarrow\dfrac{2x+1-x^2-2}{x^2+2}\ge0\)
\(\Rightarrow-x^2+2x-1\ge0\Rightarrow-\left(x-1\right)^2\ge0\)vô lí

a) Với m = 5 phương trình đã cho trở thành
x2 - 8x + 7 = 0
Dễ thấy phương trình trên có a + b + c = 0 nên có hai nghiệm phân biệt x1 = 1 ; x2 = c/a = 7
Vậy với m = 5 thì phương trình đã cho có tập nghiệm S = { 1 ; 7 }
b) Ta có : Δ = b2 - 4ac = [ -2( m - 1 ) ]2 - 4( m + 2 )
= 4( m2 - 2m + 1 ) - 4m + 8
= 4m2 - 12m + 12 = 4( m - 3/2 )2 + 3 ≥ 3 > 0 ∀ m
=> Phương trình đã cho luôn có hai nghiệm phân biệt với mọi số thực m
Theo hệ thức Viète ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m-2\\x_1x_2=\frac{c}{a}=m+2\end{cases}}\)
Ta có : \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=4\Leftrightarrow\frac{x_1^2}{x_1x_2}+\frac{x_2^2}{x_1x_2}=4\)
\(\Rightarrow x_1^2+x_2^2=4x_1x_2\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Rightarrow\left(2m-2\right)^2-6\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-8m+4-6m-12=0\Leftrightarrow2m^2-7m-4=0\)
Đến đây dễ rồi bạn tự làm tiếp heng :)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+1-x\right)=\left(x+1\right)^3-\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)\left[\left(x+1\right)^2-x\right]=\left(x+1\right)^3-\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)^3-x\left(x+1\right)=\left(x+1\right)^3-\left(x+1\right)\)
\(\Leftrightarrow x\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)