x(y-3)+2(3-y)=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2021
Câu 3:
\(\dfrac{x}{y}=\dfrac{5}{9}\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=5\\ \dfrac{y}{9}=10\Rightarrow y=90\)
Câu b:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\dfrac{x}{2}=7\Rightarrow x=14\\ \dfrac{y}{3}=7\Rightarrow y=21\)
Câu c:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-1}{5+7-10}=\dfrac{20}{2}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=50\\ \dfrac{y}{7}=10\Rightarrow y=70\\ \dfrac{z}{10}=10\Rightarrow z=100\)
Câu d:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\dfrac{x}{3}=11\Rightarrow x=3\\ \dfrac{y}{4}=11\Rightarrow y=44\\ \dfrac{z}{5}=11\Rightarrow z=55\)
Câu e:
\(\dfrac{x}{4}=\dfrac{y}{2}\Rightarrow\dfrac{x}{8}=\dfrac{y}{6}\\\dfrac{y}{3}=\dfrac{z}{5}\Rightarrow\dfrac{y}{6}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10} \)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{8+6-10}=\dfrac{20}{4}=5\)
\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{6}=5\Rightarrow y=30\\ \dfrac{z}{10}=5\Rightarrow z=50\)
25 tháng 10 2021
3) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.9=90\end{matrix}\right.\)
4) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x}{10}=\dfrac{2y}{6}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\Rightarrow\left\{{}\begin{matrix}x=7.2=14\\y=7.3=21\end{matrix}\right.\)
5) \(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-z}{5+7-10}=\dfrac{20}{2}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.7=70\\z=10.10=100\end{matrix}\right.\)
6) \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x}{9}=\dfrac{2y}{8}=\dfrac{2z}{10}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\Rightarrow\left\{{}\begin{matrix}x=11.3=33\\y=11.4=44\\z=11.5=55\end{matrix}\right.\)
7) \(\Rightarrow\dfrac{x}{12}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{12+6-10}=\dfrac{20}{8}=\dfrac{5}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}.12=30\\y=\dfrac{5}{2}.6=15\\z=\dfrac{5}{2}.10=25\end{matrix}\right.\)
13 tháng 3 2021
\(C=5x^3y^2-4x^3y^2+3x^2y^3+\dfrac{1}{2}x^2y^3+\dfrac{1}{3}x^4y^5-3x^4y^5-\dfrac{1}{7}\)
\(=x^3y^2+\dfrac{7}{2}x^2y^3-\dfrac{8}{3}x^4y^5-\dfrac{1}{7}\)
NT
2
21 tháng 6 2023
a: =2(x-y)^3/(x-y)-7(x-y)^2/(x-y)+(x-y)/(x-y)
=2(x-y)^2-7(x-y)+1
b: =3(x-y)^5/5(x-y)^2-2(x-y)^4/5(x-y)^2+3(x-y)^2/5(x-y)^2
=3/5(x-y)^3-2/5(x-y)^2+3/5
21 tháng 6 2023
\(a,\)
\(\left[2\left(x-y\right)^3-7\left(y-x\right)^2-\left(y-x\right)\right]:\left(x-y\right)\)
\(=\left[2\left(x-y\right)^3-7\left(x-y\right)^2+\left(x-y\right)\right]:\left(x-y\right)\)
\(=\left\{\left(x-y\right)\left[2\left(x-y\right)^2-7\left(x-y\right)+1\right]\right\}:\left(x-y\right)\)
\(=2\left(x-y\right)^2-7\left(x-y\right)+1\)
\(b,\)
\(\left[3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2\right]:\left[5\left(x-y\right)^2\right]\)
\(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)
Y
29 tháng 6 2023
\(1,\left(x+y\right)^2-\left(x-y\right)^2=\left[\left(x+y\right)-\left(x-y\right)\right]\left[\left(x+y\right)+\left(x-y\right)\right]=\left(x+y-x+y\right)\left(x+y+x-y\right)=2y.2x=4xy\)
\(2,\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
\(3,\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =4y^2\)
\(4,\left(2x+3\right)^2-2\left(2x+3\right)\left(2x+5\right)+\left(2x+5\right)^2\\ =\left[\left(2x+3\right)-\left(2x+5\right)\right]^2\\ =\left(2x+3-2x-5\right)^2\\ =\left(-2\right)^2\\ =4\)
\(5,9^8.2^8-\left(18^4+1\right)\left(18^4-1\right)\\ =18^8-\left[\left(18^4\right)^2-1\right]\\ =18^8-18^8+1\\ =1\)
29 tháng 6 2023
1: =x^2+2xy+y^2-x^2+2xy-y^2=4xy
2: =x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3
=6x^2y
3: =(x+y-x+y)^2=(2y)^2=4y^2
4: =(2x+3-2x-5)^2=(-2)^2=4
5: =18^8-18^8+1=1
17 tháng 10 2021
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{-32}{8}=-4\)
Do đó: x=-12; y=-20
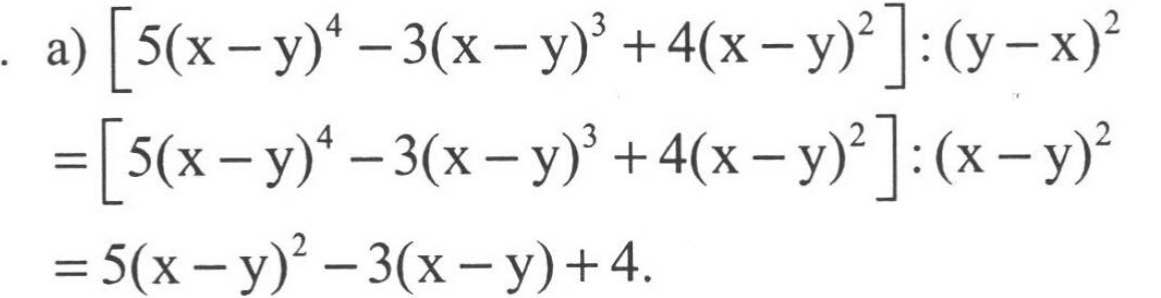
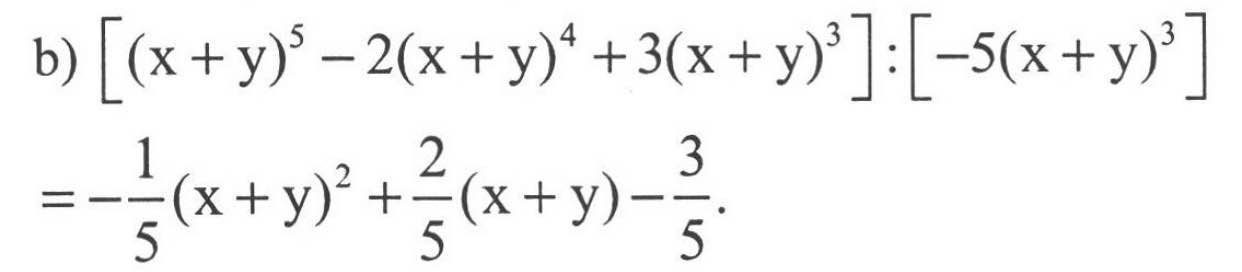
x(y - 3) + 2(3 - y) = 5
⇒ x(y - 3) - 2(y - 3) = 5
⇒ (y - 3)(x - 2) = 5 = 1.5 = 5.1 = -1.-5 = -5.-1
Ta có bảng sau: