Cho tam giác ABC, điểm M nằm trên cạnh BC. Gọi A', B', C' lần lượt là trung điểm của các đoạn thẳng MA, MB, MC (Hình 47)
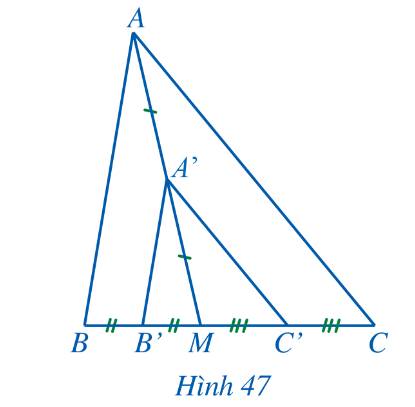
a) So sánh các cặp góc:
\( \widehat {B'A'C'} \) và \( \widehat {BAC} \); \( \widehat {C'B'A'} \) và \( \widehat {CBA} \); \( \widehat {A'C'B'} \) và \( \widehat {ACB} \).
b) So sánh các tỉ số: \( \frac{A'B'}{AB} \); \( \frac{B'C'}{BC} \); \( \frac{C'A'}{CA} \).


a) Xét tam giác ABM có A'B' là đường trung bình của tam giác
\( \Rightarrow A'B' // AB\)
\( \Rightarrow \widehat {C'B'A'} = \widehat {CBA}\) (hai góc đồng vị)
Tương tự, tam giác AMC có A'C' là đường trung bình nên \( = \widehat {ACB}\) (hai góc đồng vị)
Xét tam giác ABC có:
\( \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = 180^0\)
Xét tam giác A'B'C' có:
\( \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'} = 180^0\)
\(\Rightarrow \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'}\)
\(\Rightarrow \widehat {BAC} = \widehat {B'A'C'}\)
b) A'B' là đường trung bình của tam giác ABM nên
\(A'B' = \frac {1}{2} AB \Rightarrow \frac {A'B'}{AB} = \frac {1}{2}\)
A'B' là đường trung bình của tam giác ABM nên
\(A'C' = \frac {1}{2} AC \Rightarrow \frac {A'C'}{AC} = \frac {1}{2}\)
Ta có: \( \frac{B'C'}{BC} = \frac{MB' +MC'}{2MB' + 2MC'} = \frac{MB' +MC'}{2(MB' + MC')} = \frac{1}{2}\)
\( \Rightarrow \frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{C'A'}{CA} \)