giúp mình bài này với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
4 tháng 3 2023
Lời giải:
Thể tích của bể:
$4\times 3\times 0,5=6$ (m3)
Đổi $6$ m3 = $6000$ lít.
Mỗi phút cả 2 vòi chảy được: $85+25=110$ (lít)
Nếu cả hai vòi cùng chảy thì sẽ đầy bể sau:
$6000:110=\frac{600}{11}$ (phút)
31 tháng 8 2023
1: =>15x-3-x^2+2x+x^2-13x=7
=>4x-3=7
=>4x=10
=>x=5/2
2: =>4x+8-14x+7+27x-36=30
=>17x-21=30
=>17x=51
=>x=3
3: =>10x-16-12x+15=12x-16+11
=>-2x-1=12x-5
=>-14x=-4
=>x=2/7
4: =>3x^2-6x-3x^2-3=x^2+1-x^2+2x
=>-6x-3=2x+1
=>-8x=4
=>x=-1/2
5: =>15x+25-8x+12=5x+6x+36
=>7x+37=11x+36
=>-4x=-1
=>x=1/4
6: =>7x+7+6x^2-3x-6x^2-30x=-42
=>-26x=-49
=>x=49/26
9 tháng 7 2023
a: Xét ΔADB vuông tại D và ΔADC vuông tại D có
AB=AC
AD chung
=>ΔADB=ΔADC
=>DB=DC
c: Xét ΔABC có
D là trung điểm của BC
DK//AB
=>K là trung điểm của AC
ΔADC vuông tại D có DK là trung tuyến
nên DK=KC
=>ΔKDC cân tại K
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}=\sqrt{2^2.5}-\sqrt{3^2.5}+\sqrt{\left(\sqrt{5}+1\right)^2}=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1=1\)
\(\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}=2\sqrt{5}-2-\left|\sqrt{5}-2\right|=2\sqrt{5}-2-\sqrt{5}+2=\sqrt{5}\)
\(\left(\sqrt{27}+3\sqrt{12}-2\sqrt{3}\right):\sqrt{3}=\left(3\sqrt{3}+6\sqrt{3}-2\sqrt{3}\right):\sqrt{3}=7\sqrt{3}:\sqrt{3}=7\)
\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{5^2.2}-3\sqrt{2^2.2}+\sqrt{\left(\sqrt{2}+1\right)^2}=5\sqrt{2}-6\sqrt{2}+\sqrt{2}+1=1\)
2 tháng 8 2021
1) \(A=\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}\)
\(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1\)
=1
2) Ta có: \(B=\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=2\sqrt{5}-2-\sqrt{5}+2\)
\(=\sqrt{5}\)
8 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
Độ dài đáy của hình bình hành đó là:
`12 \times 2 = 24 (cm)`
S của hình bình hành đó là:
`12 \times 24 =288 (cm^2)`
Đáp số: `288 cm^2.`
8 tháng 8 2023
Giải :
Độ dài cạnh đáy là :
12 x 3 = 26 ( m )
Diện tích hình bình hành là :
12 x 36 = 432 ( m2 )
Đ/s :..............
8 tháng 6 2021
a)Đk:\(x\ne4\)
\(\dfrac{x^4}{4-x}+x^3+1=\dfrac{x^4+\left(x^3+1\right)\left(4-x\right)}{4-x}\)\(=\dfrac{x^4+\left(-x^4+4x^3+4-x\right)}{4-x}=\dfrac{4x^3-x+4}{4-x}\)
b) Đk: \(x\ne0;x\ne1\)
\(\dfrac{1}{x^2-x}+\dfrac{2x}{x-1}=\dfrac{1}{x\left(x-1\right)}+\dfrac{2x^2}{x\left(x-1\right)}=\dfrac{1+2x^2}{x\left(x-1\right)}\)
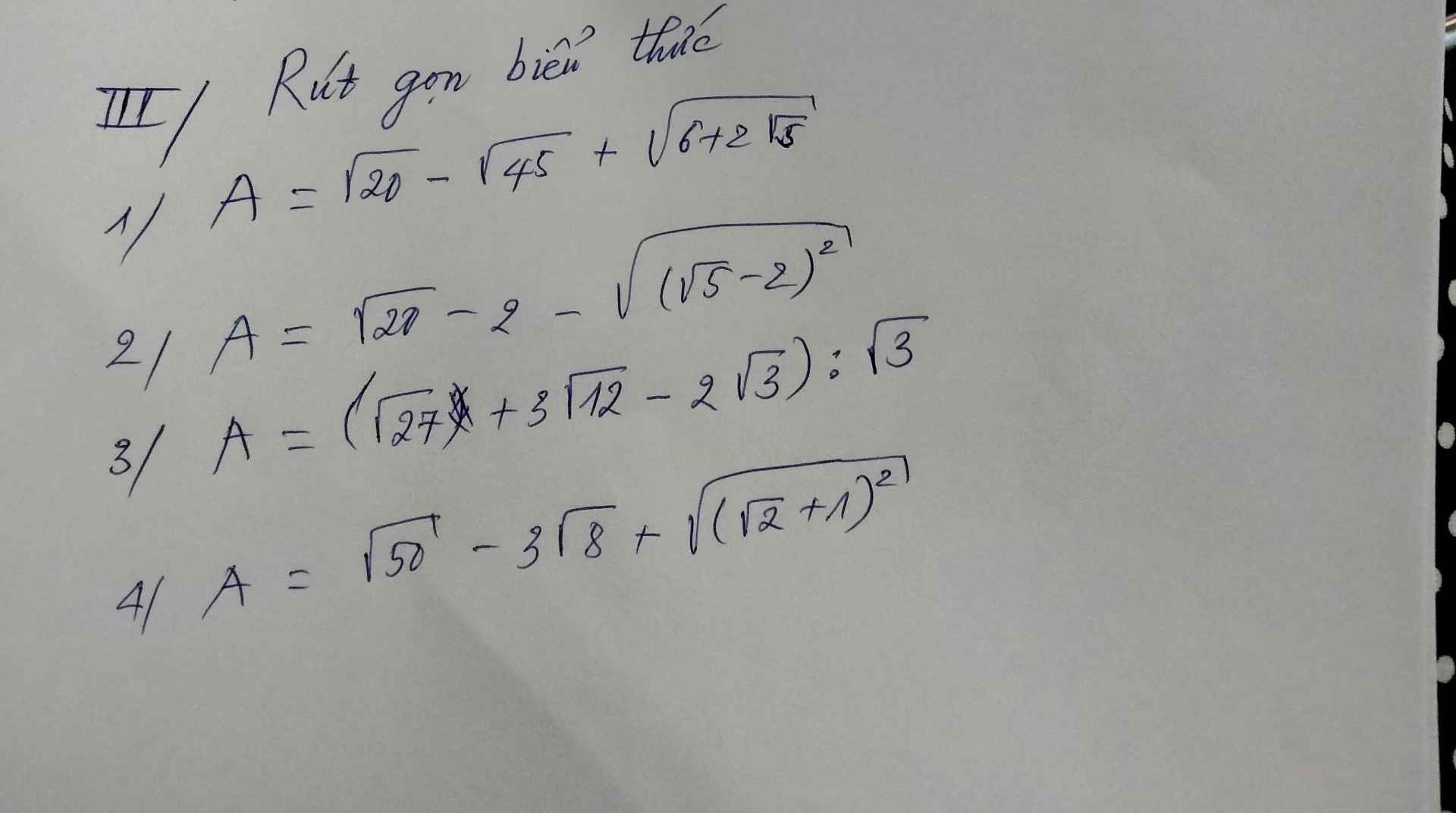
1 D
2 C
3 D
6 C
7 D
8 A
9 D
10 C
11 C
12 D
13 B
3D 4C 5D 6C 7D 8A 9D 10C 11C 12C 13B