1/ cho đường tròn (O) và 2 điểm A,B nằm bên trong (O), A,O,B không thẳng hàng. hãy dựng 2 dây song song và bằng nhau sao cho A thuộc 1 dây, B thuộc dây còn lại.
giúp mjk nha m.n^^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

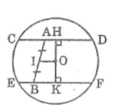
* Cách dựng
- Dựng trung điểm I của AB
- Qua A dựng dây CD song song với OI
- Qua B dựng dây EF song song với OI
Ta được CD và EF là hai dây cần dựng
* Chứng minh
Ta có : CD // OI, EF // OI
Suy ra : CD // EF
Kẻ OH ⊥ CD cắt EF tại K
Suy ra: OK ⊥ EF
Lại có: IA = IB
Suy ra: OH = OK
Vậy CD = EF.

Ta có:
- Vì ON = OP < R/2, nên N và P nằm trong đường tròn tâm O, nên A, C, B, D đều nằm trên đường tròn (O).
- Vì AC // BD, nên theo định lí của dây cung, ta có: AM = MC và BM = MD.
- Ta có: ∠BAC = ∠BMC (do ABMC là hình bình hành) và ∠ACB = ∠AMB (do ABMC là hình bình hành).
- Vậy tứ giác ABMC là tứ giác cùng tứ giác nội tiếp, nên ta có: ∠BMC + ∠AMB = 180°.
- Từ đó, ta có: ∠BAC + ∠ACB = 180°.
- Vậy tứ giác ABCD là tứ giác điều hòa.
- Gọi K' là giao điểm của BD và AO. Ta cần chứng minh K', Q, A đồng quy.
- Ta có: ∠QAC = ∠QDC (do AC // BD) và ∠QCA = ∠QCB (do ABMC là hình bình hành).
- Vậy tứ giác AQCD là tứ giác cùng tứ giác nội tiếp, nên ta có: ∠QDC + ∠QCA = 180°.
- Từ đó, ta có: ∠QAC + ∠QCA = 180°.
- Vậy tứ giác AQCK' là tứ giác điều hòa.
- Vậy K', Q, A đồng quy. - Vậy KQ, BD, AO đồng quy.\
Xin tick!!